如图,在平面直角坐标系中,直线y=2x与反比例函数 在第一象限内的图象交于点A(m,2),将直线y=2x向下平移后与反比例函数 在第一象限内的图象交于点P,且△POA的面积为2.
(1)求k的值.
(2)求平移后的直线的函数解析式.

如图,将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开,得到△ACD,再将△ACD沿DB方向平移到△A′C′D′的位置,若平移开始后点D′未到达点B时,A′C′交CD于E,D′C′交CB于点F,连接EF,当四边形EDD′F为菱形时,试探究△A′DE的形状,并判断△A′DE与△EFC′是否全等?请说明理由.
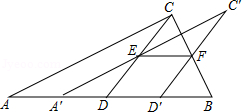
如图,在 中, .将 沿着 方向平移得到 ,其中点 在边 上, 与 相交于点 .
(1)求证: 为等腰三角形;
(2)连接 、 、 ,当点 在什么位置时,四边形 为矩形,并说明理由.

如图,已知 A(6,0), B(8,5),将线段 OA平移至 CB,点 D在 x轴正半轴上(不与点 A重合),连接 OC, AB, CD, BD.
(1)求对角线 AC的长;
(2)设点 D的坐标为( x,0),△ ODC与△ ABD的面积分别记为 S 1, S 2.设 S= S 1﹣ S 2,写出 S关于 x的函数解析式,并探究是否存在点 D使 S与△ DBC的面积相等?如果存在,用坐标形式写出点 D的位置;如果不存在,说明理由.

在平面直角坐标系中,为原点,点
,点
在
轴的正半轴上,
.矩形
的顶点
,
,
分别在
,
,
上,
.
(Ⅰ)如图①,求点的坐标;
(Ⅱ)将矩形沿
轴向右平移,得到矩形
,点
,
,
,
的对应点分别为
,
,
,
.设
,矩形
与
重叠部分的面积为
.
①如图②,当矩形与
重叠部分为五边形时,
,
分别与
相交于点
,
,试用含有
的式子表示
,并直接写出
的取值范围;
②当时,求
的取值范围(直接写出结果即可).

如图1,在 中, 于点 , 的垂直平分线交 于点 ,交 于点 , , , .
(1)如图2,作 于点 ,交 于点 ,将 沿 方向平移,得到△ ,连接 .
①求四边形 的面积;
②直线 上有一动点 ,求 周长的最小值.
(2)如图3,延长 交 于点 ,过点 作 ,过 边上的动点 作 ,并与 交于点 ,将 沿直线 翻折,使点 的对应点 恰好落在直线 上,求线段 的长.

已知反比例函数 .
(1)若该反比例函数的图象与直线 只有一个公共点,求k的值;
(2)如图,反比例函数 的图象记为曲线C1,将C1向左平移2个单位长度,得曲线C2,请在图中画出C2,并直接写出C1平移至C2处所扫过的面积.
在 中, , 交 的延长线于点 .

特例感知:
(1)将一等腰直角三角尺按图1所示的位置摆放,该三角尺的直角顶点为 ,一条直角边与 重合,另一条直角边恰好经过点 .通过观察、测量 与 的长度,得到 .请给予证明.
猜想论证:
(2)当三角尺沿 方向移动到图2所示的位置时,一条直角边仍与 边重合,另一条直角边交 于点 ,过点 作 垂足为 .此时请你通过观察、测量 、 与 的长度,猜想并写出 、 与 之间存在的数量关系,并证明你的猜想.
联系拓展:
(3)当三角尺在图2的基础上沿 方向继续移动到图3所示的位置(点 在线段 上,且点 与点 不重合)时,请你判断(2)中的猜想是否仍然成立?(不用证明)
如图1,点、点
在直线
上,反比例函数
的图象经过点
.

(1)求和
的值;
(2)将线段向右平移
个单位长度
,得到对应线段
,连接
、
.
①如图2,当时,过
作
轴于点
,交反比例函数图象于点
,求
的值;
②在线段运动过程中,连接
,若
是以
为腰的等腰三角形,求所有满足条件的
的值.
边长为6的等边 中,点 、 分别在 、 边上, , .
(1)如图1,将 沿射线 方向平移,得到△ ,边 与 的交点为 ,边 与 的角平分线交于点 ,当 多大时,四边形 为菱形?并说明理由.
(2)如图2,将 绕点 旋转 ,得到△ ,连接 、 .边 的中点为 .
①在旋转过程中, 和 有怎样的数量关系?并说明理由;
②连接 ,当 最大时,求 的值.(结果保留根号)

在一次数学研究性学习中,小兵将两个全等的直角三角形纸片 和 拼在一起,使点 与点 重合,点 与点 重合(如图 ,其中 , , ,并进行如下研究活动.
活动一:将图1中的纸片 沿 方向平移,连结 , (如图 ,当点 与点 重合时停止平移.
[思考]图2中的四边形 是平行四边形吗?请说明理由.
[发现]当纸片 平移到某一位置时,小兵发现四边形 为矩形(如图 .求 的长.
活动二:在图3中,取 的中点 ,再将纸片 绕点 顺时针方向旋转 度 ,连结 , (如图 .
[探究]当 平分 时,探究 与 的数量关系,并说明理由.

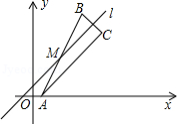
如图,直线与双曲线
相交于点
.已知点
,
,连接
,将
沿
方向平移,使点
移动到点
,得到△
.过点
作
轴交双曲线于点
.
(1)求与
的值;
(2)求直线的表达式;
(3)直接写出线段扫过的面积.

对于坐标平面内的点,现将该点向右平移1个单位,再向上平移2个单位,这种点的运动称为点 的斜平移,如点 经1次斜平移后的点的坐标为 ,已知点 的坐标为 .
(1)分别写出点 经1次,2次斜平移后得到的点的坐标.
(2)如图,点 是直线 上的一点,点 关于点 的对称点为点 ,点 关于直线 的对称点为点 .
①若 、 、 三点不在同一条直线上,判断 是否是直角三角形?请说明理由.
②若点 由点 经 次斜平移后得到,且点 的坐标为 ,求出点 的坐标及 的值.
我们在学完“平移、轴对称、旋转”三种图形的变化后,可以进行进一步研究,请根据示例图形,完成下表.
图形的变化 |
示例图形 |
与对应线段有关的结论 |
与对应点有关的结论 |
平移 |
|
(1) |
|
轴对称 |
|
(2) |
(3) |
旋转 |
|
;对应线段 和 所在的直线相交所成的角与旋转角相等或互补. |
(4) |
试题篮
()