如图,在 轴的正半轴上依次截取OA1=A1A2=A2A3=A3A4=A4A5,过点A1、A2、A3、A4、A5分别作x轴的垂线与反比例函数
轴的正半轴上依次截取OA1=A1A2=A2A3=A3A4=A4A5,过点A1、A2、A3、A4、A5分别作x轴的垂线与反比例函数 的图象相交于点P1、P2、P3、P4、P5,得直角三角形OP1A1、A1P2A2、A2P3A3、A3P4A4、A4P5A5,并设其面积分别为S1、S2、S3、S4、S5,则S5的值为 .
的图象相交于点P1、P2、P3、P4、P5,得直角三角形OP1A1、A1P2A2、A2P3A3、A3P4A4、A4P5A5,并设其面积分别为S1、S2、S3、S4、S5,则S5的值为 .
已知二次函数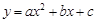 的图象如图所示,那么一次函数
的图象如图所示,那么一次函数 和反比例函数
和反比例函数 在同一平面直角坐标系中的图象大致是【 】
在同一平面直角坐标系中的图象大致是【 】 A.
A. B.
B. C.
C.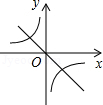 D
D
如图,一次函数 的图像与反比例函数
的图像与反比例函数 的图像交于
的图像交于 两点,与
两点,与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 ,已知
,已知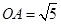 ,点
,点 的坐标为
的坐标为 ,过点
,过点 作
作 轴,垂足为
轴,垂足为 。
。
(1)求反比例函数和一次函数的解析式;
(2)求 的面积。
的面积。
(3)根据图像回答:当x 为何值时,一次函数的函数值大于
反比例函数的函数值?
如图,在平面直角坐标系xOy中,直线AB与x轴、y轴分别交于点A,B,与反比例函数 (
( 为常数,且
为常数,且 )在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若
)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若 (
( 为大于l的常数).记△CEF的面积为
为大于l的常数).记△CEF的面积为 ,△OEF的面积为
,△OEF的面积为 ,则
,则 =________. (用含
=________. (用含 的代数式表示)
的代数式表示)
实践与探究:
对于任意正实数a、b,∵ ≥0, ∴
≥0, ∴ ≥0,∴
≥0,∴ ≥
≥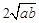
只有当a=b时,等号成立。
结论:在 ≥
≥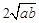 (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥ ,只有当a=b时,a+b有最小值
,只有当a=b时,a+b有最小值 。 根据上述内容,回答下列问题:
。 根据上述内容,回答下列问题:
(1)若m>0,只有当m= 时,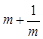 有最小值 ;
有最小值 ;
若m>0,只有当m= 时,2 有最小值 .
有最小值 .
(2)如图,已知直线L1: 与x轴交于点A,过点A的另一直线L2与双曲线
与x轴交于点A,过点A的另一直线L2与双曲线 相交于点B(2,m),求直线L2的解析式.
相交于点B(2,m),求直线L2的解析式.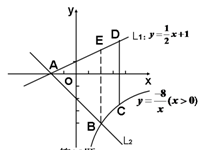
(3)在(2)的条件下,若点C为双曲线上任意一点,作CD∥y轴交直线L1
于点D,试求当线段CD最短时,点A、B、C、D围成的四边形面积.
阅读理解:对于任意正实数a、b,∵(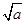 -
-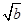 )2≥0,∴a-2
)2≥0,∴a-2 +b≥0,∴a+b≥2
+b≥0,∴a+b≥2 ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.
结论:在a+b≥2 (a、b均为正实数)中,若ab为定值p,则a+b≥2
(a、b均为正实数)中,若ab为定值p,则a+b≥2 ,只有当a=b时,a+b有最小值2
,只有当a=b时,a+b有最小值2 . 根据上述内容,回答下列问题:
. 根据上述内容,回答下列问题:
(1)若m>0,只有当m= 时,m+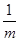 有最小值 ;
有最小值 ;
若m>0,只有当m= 时,2m+ 有最小值 .
有最小值 .
(2)如图,已知直线L1:y= x+1与x轴交于点A,过点A的另一直线L2与双曲线y=
x+1与x轴交于点A,过点A的另一直线L2与双曲线y=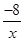
(x>0)相交于点B(2,m),求直线L2的解析式.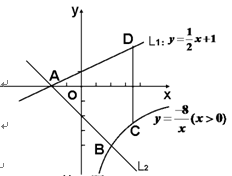
(3)在(2)的条件下,若点C为双曲线上任意一点,作CD∥y轴交直线L1于点D,试
求当线段CD最短时,点A、B、C、D围成的四边形面积.
如图,已知抛物线 经过O(0,0),A(4,0),B(3,
经过O(0,0),A(4,0),B(3, )三点,连接AB,过点B作BC∥
)三点,连接AB,过点B作BC∥ 轴交该抛物线于点C.
轴交该抛物线于点C.

求这条抛物线的函数关系式.
两个动点P、Q分别从O、A同时出发,以每秒1个单位长度的速度运动. 其中,点P沿着线段0A向A点运动,点Q沿着线段AB向B点运动. 设这两个动点运动的时间为
 (秒) (0<
(秒) (0< ≤2),△PQA的面积记为S.
≤2),△PQA的面积记为S.
① 求S与 的函数关系式;
的函数关系式;
② 当 为何值时,S有最大值,最大值是多少?并指出此时△PQA的形状;
为何值时,S有最大值,最大值是多少?并指出此时△PQA的形状;
是否存在这样的
 值,使得△PQA是直角三角形?若存在,请直接写出此时P、Q两点的坐标;若不存在,请说明理由.
值,使得△PQA是直角三角形?若存在,请直接写出此时P、Q两点的坐标;若不存在,请说明理由.
如图,Rt△ABO的顶点A是双曲线 与直线
与直线 在第二象限的交点,AB⊥
在第二象限的交点,AB⊥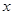 轴于B且S△ABO=
轴于B且S△ABO=

求这两个函数的解析式
求直线与双曲线的两个交点A,C的坐标和△AOC的面积。
如图,半径为5的⊙P与x轴交于点M(0,-4),N(0,-10). 函数y= (x<0)的图
(x<0)的图
象过点P,则下列说法正确的有 .(填序号)
①⊙P与x轴相离; ②△PMN的面积为14;
③⊙P的坐标为(-4,-7); ④k的值为28.
(本小题满分8分)如图,一次函数 的图象分别交x轴、y轴于A、
的图象分别交x轴、y轴于A、
B两点,P为AB上一点且PC为△AOB的中位线,PC的延长线交反比例函数
的图象于Q, .
.
(1)求P点坐标;
(2)求Q点坐标;
(3)求出反比例函数解析式。
平面直角坐标系中,直线AB交x轴于点A,交y轴于点B且与反比例函数图像分别交于C、D两点,过点C作CM x轴于M,AO=6,BO=3,CM=5。求直线AB的解析式和反比例函数解析式。
x轴于M,AO=6,BO=3,CM=5。求直线AB的解析式和反比例函数解析式。
如图,矩形ABCD的边AB与y轴平行,顶点A的坐标为(1,2),点B与点D在反比例函数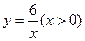 的图象上,则点C的坐标为 .
的图象上,则点C的坐标为 .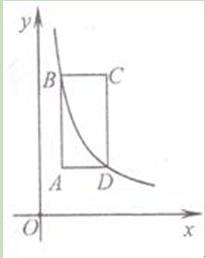
(11·贺州)
如图,在平面直角坐标系中,点O为原点,反比例函数 的图象经过点(1,4),菱
的图象经过点(1,4),菱
形OABC的顶点A在函数的图象上,对角线OB在x轴上.
(1)求反比例函数的关系式;
(2)直接写出菱形OABC的面积.
试题篮
()