初中数学平行线分线段成比例解答题

在平面直角坐标系中，我们不妨把纵坐标是横坐标的2倍的点称之为“理想点”，例如点（﹣2，﹣4），（1，2），（3，6）…都是“理想点”，显然这样的“理想点”有有无数多个．
（1）若点M（2，a）是反比例函数（k为常数，）图象上的“理想点”，求这个反比例函数的表达式；
（2）函数（m为常数，）的图象上存在“理想点”吗？若存在，请求出“理想点”的坐标；若不存在，请说明理由．

已知直线y=﹣3x与双曲线y=交于点P （﹣1，n）．
（1）求m的值；
（2）若点A （，），B（，）在双曲线y=上，且＜＜0，试比较，的大小．

如图，在平面直角坐标系xOy中，直线y=﹣x+b与x轴交于点A，与双曲线y=﹣在第二象限内交于点B（﹣3，a）．

（1）求a和b的值；
（2）过点B作直线l平行x轴交y轴于点C，求△ABC的面积．

如图，已知反比例函数y=（x＞0，k是常数）的图象经过点A（1，4），点B（m，n），其中m＞1，AM⊥x轴，垂足为M，BN⊥y轴，垂足为N，AM与BN的交点为C．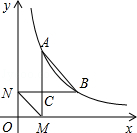

（1）写出反比例函数解析式；
（2）求证：△ACB∽△NOM；
（3）若△ACB与△NOM的相似比为2，求出B点的坐标及AB所在直线的解析式．

小明在学习反比例函数的图象时，他的老师要求同学们根据“探索一次函数y₁=x+1的图象”的基本步骤，在纸上逐步探索函数y₂=的图象，并且在黑板上写出4个点的坐标：A（，），B（1，2），C（1，），D（﹣2，﹣1）．
（1）在A、B、C、D四个点中，任取一个点，这个点既在直线y₁=x+1又在双曲线y₂=上的概率是多少？
（2）小明从A、B、C、D四个点中任取两个点进行描点，求两点都落在双曲线y₂=上的概率．

如图，已知直线y=2x分别与双曲线y=，y=（x＞0）交于P、Q两点，且OP=2OQ，点A是双曲线y=上的动点，过A作AB∥x轴，AC∥y轴，分别交双曲线y=（x＞0）于点B、C．连接BC．

（1）求k的值；
（2）随着点A的运动，△ABC的面积是否发生变化？若不变，求出△ABC的面积，若改变，请说明理由．
（3）直线y=2x上是否存在点D，使得点A、B、C、D为顶点的四边平行四边形？若能，求出相应点A的坐标；若不能，请说明理由．

如图，一次函数的图象与x轴、y轴分别相交于A、B两点，且与反比例函数（）的图象在第一象限交于点C，如果点B的坐标为（0，2），OA=OB，B是线段AC的中点．

（1）求点A的坐标及一次函数解析式．
（2）求点C的坐标及反比例函数的解析式．

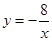如图，已知一次函数的图象与反比例函数的图象交于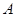，两点，且点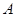的横坐标和点的纵坐标都是．

求：（1）一次函数解析式；
（2）求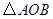的面积．

如图，已知点A（a，3）是一次函数y₁=x+b图象与反比例函数y₂=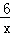图象的一个交点．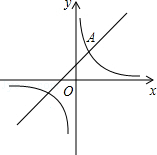

（1）求一次函数的解析式；
（2）在y轴的右侧，当y₁＞y₂时，直接写出x的取值范围．

如图，已知A（-4，0．5），B（-1，2）是一次函数y=ax+b与反比例函数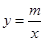（m＜0）图象的两个交点，AC⊥x轴于C，BD⊥y轴于D．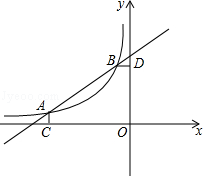 

（1）根据图象直接回答：在第二象限内，当x取何值时，一次函数大于反比例函数的值？
（2）求一次函数解析式及m的值；
（3）P是线段AB上的一点，连接PC，PD，若△PCA和△PDB面积相等，求点P坐标．

如图，函数的图象与函数（）的图象交于A（，1）B（1，）两点．

（1）求函数的表达式；    
（2）观察图象，比较当时，与的大小．

如图，A、B是双曲线y=上的两点，过A点作AC⊥x轴，交OB于D点，垂足为C，过B点作BE⊥x轴，垂足为E．若△ADO的面积为1，D为OB的中点，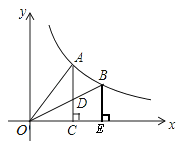

（1）求四边形DCEB的面积。
（2）求k的值。

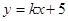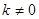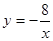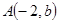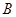如图，一次函数（为常数，且）的图像与反比例函数的图像交于，两点．

（1）求一次函数的表达式；
（2）若将直线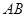向下平移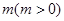个单位长度后与反比例函数的图像有且只有一个公共点，求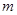的值．

如图，在平面直角坐标系中，矩形OABC的顶点A，C分别在x轴，y轴上，函数y=的图象过点P（4，3）和矩形的顶点B（m，n）（0＜m＜4）．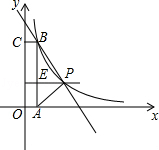

（1）求k的值；
（2）连接PA，PB，若△ABP的面积为6，求直线BP的解析式．

（本小题满分13分）如图，矩形OABC的顶点A、C分别在x轴和y轴上，点B的坐标为（2，3），双曲线，的图像经过BC上的点D与AB交于点E，连接DE，若若E是AB的中点﹒

（1）求D点的坐标；
（2）点F是OC边上一点，若△FBC和△DEB相似，求BF的解析式；
（3）若点P（m，3m+6）也在此反比例函数的图像上（其中m >0），过p点作x轴的垂线，交x轴于点M，若线段PM上存在一点Q，使得△OQM的面积是，设Q点的纵坐标为n，求的值．