如图,直线y=mx与双曲线y= 相交于A、B两点,A点的坐标为(1,2)
相交于A、B两点,A点的坐标为(1,2)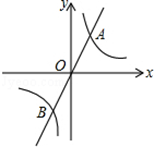
(1)求反比例函数的表达式;
(2)根据图象直接写出当mx> 时,x的取值范围;
时,x的取值范围;
(3)计算线段AB的长.
如图,一次函数的图象与x轴,y轴分别相交于A,B两点,且与反比例函数y=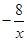 的图象在第二象限交于点C,其中点A(2,0),点B是AC的中点.
的图象在第二象限交于点C,其中点A(2,0),点B是AC的中点.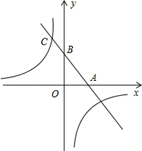
(1)求点C的坐标;
(2)求一次函数的解析式.
反比例函数y= 的图象经过点A(4,-2),
的图象经过点A(4,-2),
(1)求这个函数的解析式;
(2)请判断点B(1,8)是否在这个反比例函数的图象上,并说明理由.
(3)当1<x<2时,直接写出y 的取值范围:
如图,一次函数 的图象与反比例函数
的图象与反比例函数 (
( 为常数,且
为常数,且 )的图象都经过点A(m,2).
)的图象都经过点A(m,2).
(1)求点A的坐标及反比例函数的表达式;
(2)设一次函数 的图象与x轴交于点B,若点P是x轴上一点,且满足△ABP的面积是2,直接写出点P的坐标.
的图象与x轴交于点B,若点P是x轴上一点,且满足△ABP的面积是2,直接写出点P的坐标.
给出如下规定:两个图形G1和G2,点P为G1上任一点,点Q为G2上任一点,如果线段PQ的长度存在最小值,就称该最小值为两个图形G1和G2之间的距离.在平面直角坐标系xOy中,O为坐标原点.
(1)点A的坐标为 ,则点
,则点 和射线OA之间的距离为________,点
和射线OA之间的距离为________,点 和射线OA之间的距离为________;
和射线OA之间的距离为________;
(2)如果直线 和双曲线
和双曲线 之间的距离为
之间的距离为 ,那么k= ;(可在图1中进行研究)
,那么k= ;(可在图1中进行研究)
(3)点E的坐标为(1, ),将射线OE绕原点O逆时针旋转60°,得到射线OF,在坐标平面内所有和射线OE,OF之间的距离相等的点所组成的图形记为图形M.
),将射线OE绕原点O逆时针旋转60°,得到射线OF,在坐标平面内所有和射线OE,OF之间的距离相等的点所组成的图形记为图形M.
①请在图2中画出图形M,并描述图形M的组成部分;(若涉及平面中某个区域时可以用阴影表示)
②将射线OE,OF组成的图形记为图形W,抛物线 与图形M的公共部分记为图形N,请直接写出图形W和图形N之间的距离.
与图形M的公共部分记为图形N,请直接写出图形W和图形N之间的距离.
设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m.n]上的“闭函数”.如函数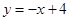 ,当x=1时,y=3;当x=3时,y=1,即当
,当x=1时,y=3;当x=3时,y=1,即当 时,有
时,有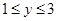 ,所以说函数
,所以说函数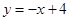 是闭区间[1,3]上的“闭函数”.
是闭区间[1,3]上的“闭函数”.
(1)反比例函数y= 是闭区间[1,2015]上的“闭函数”吗?请判断并说明理由;
是闭区间[1,2015]上的“闭函数”吗?请判断并说明理由;
(2)若二次函数y= 是闭区间[1,2]上的“闭函数”,求k的值;
是闭区间[1,2]上的“闭函数”,求k的值;
(3)若一次函数 (
( )是闭区间[m,n]上的“闭函数”,求此函数的解析式(用含m,n的代数式表示).
)是闭区间[m,n]上的“闭函数”,求此函数的解析式(用含m,n的代数式表示).
【阅读理解】对于任意正实数a、b,因为 ≥0,所以
≥0,所以
 ≥0,所以
≥0,所以 ≥
≥ ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.
【获得结论】在 ≥2
≥2 (a、b均为正实数)中,若ab为定值p,则
(a、b均为正实数)中,若ab为定值p,则 ≥2
≥2 ,只有当a=b时,
,只有当a=b时, 有最小值2
有最小值2 .
.
根据上述内容,回答下列问题:若 >0,只有当
>0,只有当 = 时,
= 时, +
+ 有最小值 .
有最小值 .
【探索应用】如图,已知A(-3,0),B(0,-4),P为 双曲线 上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D。求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D。求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
如图,反比例函数 的图象与一次函数
的图象与一次函数 的图象交于
的图象交于 ,
, 两点.(1)求反比例函数与一次函数的解析式;(2)根据图象回答:当
两点.(1)求反比例函数与一次函数的解析式;(2)根据图象回答:当 取何值时,反比例函数的值大于一次函数的值
取何值时,反比例函数的值大于一次函数的值
(本题12分)如图,一次函数 与反比例函数
与反比例函数 的图象交于A(2,3),B(-3,n)两点.
的图象交于A(2,3),B(-3,n)两点.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为C,求 .
.
如图,学校打算用材料围建一个面积为18平方米的矩形ABCD的生物园,用来饲养小兔,其中矩形ABCD的一边AB靠墙,墙长为8米,设AD的长为y米, CD的长为x米.
(1)求y与x之间的函数表达式;
(2)若围成矩形ABCD的生物园的三边材料总长不超过18米,材料AD和DC的长都是整米数,求出满足条件的所有围建方案.
直线y=x+b与x轴交于点C(4,0),与 轴交于点B,并与双曲线y=
轴交于点B,并与双曲线y= (x<0)交于点A(-1,n)。
(x<0)交于点A(-1,n)。
(1)求直线与双曲线的解析式。
(2)连接OA,求∠OAB的正弦值。
(3)若点D在x轴的正半轴上,是否存在以点D、C、B构成的三角形与△OAB相似?若存在求出D点的坐标,若不存在,请说明理由。
如图,直线 与双曲线
与双曲线 (k>0,x>0)交于点A,将直线
(k>0,x>0)交于点A,将直线 向上平移4个单位长度后,与y轴交于点C,与双曲线
向上平移4个单位长度后,与y轴交于点C,与双曲线 (k>0,x>0)交于点B.
(k>0,x>0)交于点B.
(1)设点B的横坐标分别为b,试用只含有字母b 的代数式表示k;
(2)若OA=3BC,求k的值.
如图,已知一次函数 与反比例函数
与反比例函数 的图象交于两点A(-1,6),B(a,3).
的图象交于两点A(-1,6),B(a,3).
(1)求两个函数的解析式;
(2)结合图形,直接写出时 -
- ﹥0时
﹥0时 的取值范围;
的取值范围;
(3)如图2,梯形OBCE中,BC∥OE,过点C作CE⊥x轴于点E,CE和反比例函数的图象交于点P,当梯形OBCE的面积为9时,请求出点P的坐标.
如图,已知正比例函数y= x的图象与反比例函数y=
x的图象与反比例函数y= (k>0)的图象交于A、B两点,
(k>0)的图象交于A、B两点,
且点A的横坐标为4.
(1)求k的值;
(2)根据图象直接写出正比例函数值小于反比例函数值时x的取值范围;
(3)过原点O的另一条直线l交双曲线y= (k>0)于P、Q两点(P点在第一象限),若由点A、P、B、Q为顶点组成的四边形面积为24,求点P的坐标.
(k>0)于P、Q两点(P点在第一象限),若由点A、P、B、Q为顶点组成的四边形面积为24,求点P的坐标.
试题篮
()