(本小题满分10分)已知反比例函数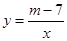 的图象的一支位于第一象限.
的图象的一支位于第一象限.
(1)判断该函数图象的另一支所在的象限,并求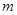 的取值范围;
的取值范围;
(2)如图8,O为坐标原点,点A在该反比例函数位于第一象限的图象上,点B与点A关于 轴对称,若
轴对称,若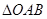 的面积为6,求
的面积为6,求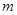 的值.
的值.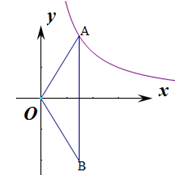
如图,直线y=x+b(b≠0)交坐标轴于A、B两点,交双曲线y= 于点D,过D作两坐标轴的垂线DC、DE,连接OD.
于点D,过D作两坐标轴的垂线DC、DE,连接OD.
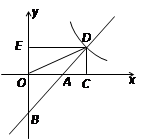
(1)求证:AD平分∠CDE;
(2)对任意的实数b(b≠0),求证AD·BD为定值;
(3)是否存在直线AB,使得四边形OBCD为平行四边形?若存在,求出直线的解析式;若不存在,请说明理由.
如图,正方形ABCO的顶点A,C分别在x轴,y轴上,O为坐标原点,点B在第二象限,边长为m,双曲线线y=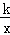 (x≠0)经过BC的中点H.
(x≠0)经过BC的中点H.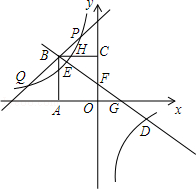
(1)用m的代数式表示出k;
(2)当m=3时,过B作直线BD,分别交x轴,y轴于G、F,分别交双曲线线y= (x≠0)的两个分支于E、D,求证:GE=DF;
(x≠0)的两个分支于E、D,求证:GE=DF;
(3)在(2)的前提下,将直线BD绕点B旋转适当的角度在第二象限与双曲线线y= (x≠0)交于P、Q,分别过P、Q作直线AC的垂线PM、QN,垂足为M、N,试探究PQ与PM+QN的数量关系并证明.
(x≠0)交于P、Q,分别过P、Q作直线AC的垂线PM、QN,垂足为M、N,试探究PQ与PM+QN的数量关系并证明.
如图,点A(m,m+1),B(m+1,2m-3)都在反比例函数 的图象上.
的图象上.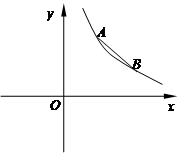
(1)求m,k的值;
(2)如果M为x轴上一点,N为y轴上一点, 以点A,B,M,N为顶点的四边形是平行四边形,试求直线MN的函数表达式.
(本小题10分)平面直角坐标系中,点A在函数y1=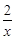 (x>0)的图象上,点B在y2=-
(x>0)的图象上,点B在y2=-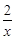 (x<0)的图象上,设A的横坐标为a,B的横坐标为b:
(x<0)的图象上,设A的横坐标为a,B的横坐标为b: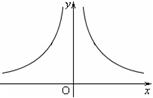
(1)当|a|=|b|=5时,求△OAB的面积;
(2)当AB∥x轴时,求△OAB的面积;
(3)当△OAB是以AB为底边的等腰三角形,且AB与x轴不平行时,求a·b的值.
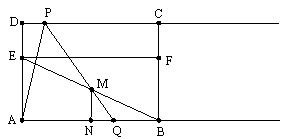
如图,在矩形ABCD中,AB=6,AD= ,点E是AD的三等分点,且AE
,点E是AD的三等分点,且AE DE,过点E作EF∥AB交BC于F,并作射线DC和AB,点P、Q分别是射线DC和射线AB上动点,点P以每秒1个单位的速度向右平移,且始终满足∠PQA=60°,设P点运动的时间为
DE,过点E作EF∥AB交BC于F,并作射线DC和AB,点P、Q分别是射线DC和射线AB上动点,点P以每秒1个单位的速度向右平移,且始终满足∠PQA=60°,设P点运动的时间为 .
.
(1)当点Q与点B重合时,求DP的长度;
(2)设AB的中点为N,PQ与线段BE相交于点M,是否存在点P,使△ 为等腰三角形?若存在,请直接写出时间
为等腰三角形?若存在,请直接写出时间 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)设△ 与四边形
与四边形 的重叠部分的面积为S,试求S与
的重叠部分的面积为S,试求S与 的函数关系式和相应的自变量
的函数关系式和相应的自变量 的取值范围.
的取值范围.
直线y=x+b与x轴交于点C(4,0),与y轴交于点B,并与双曲线 (x<0)交于点A(-1,n).
(x<0)交于点A(-1,n).
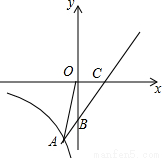
(1)求直线与双曲线的解析式;
(2)连接OA,求∠OAB的正弦值;(提示:过O点作OM垂直AC)
(3)若点D在x轴的正半轴上,是否存在以点D,C,B构成的三角形与△OAB相似?若存在,求出点D的坐标;若不存在,请说明理由.
为了预防H7N9禽流感,某学校对教室采用药熏消毒法进行消毒.已知,药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物燃烧后,y与x成反比例(如图所示).现测得药物4分钟燃毕,此室内空气中每立方米的含药量为8毫克,请你根据题中所提供的信息,解答下列问题:
(1)求出药物燃烧时与药物燃烧后y与x的函数关系式,并写出相应的自变量的取值范围 。
(2)研究表明,当空气中每立方米的含药量不低于2毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?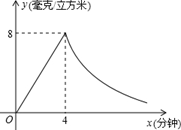
如图,在平面直角坐标系中,反比例函数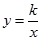 (
(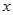 >0)的图象和矩形ABCD的第一象限,AD平行于
>0)的图象和矩形ABCD的第一象限,AD平行于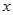 轴,且AB=2,AD=4,点A的坐标为(2,6) .
轴,且AB=2,AD=4,点A的坐标为(2,6) .
(1)直接写出B、C、D三点的坐标;
(2)若将矩形向下平移,矩形的两个顶点恰好同时落在反比例函数的图象上,猜想这是哪两个点,并求矩形的平移距离和反比例函数的解析式.
问题:如图,在 中, , , , 的平分线 , 分别与直线 交于点 , ,求 的长.
答案: .
探究:(1)把"问题"中的条件" "去掉,其余条件不变.
①当点 与点 重合时,求 的长;
②当点 与点 重合时,求 的长.
(2)把"问题"中的条件" , "去掉,其余条件不变,当点 , , , 相邻两点间的距离相等时,求 的值.
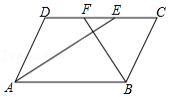
已知:如图,在菱形 中,点 、 分别在边 、 上, , 的延长线交 的延长线于点 , 的延长线交 的延长线于点 .
[小题1]求证: ;
[小题2]如果 ,求证: .
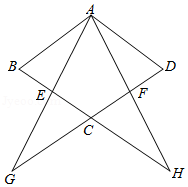
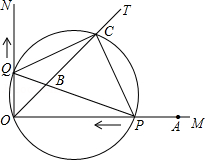
如图,已知 , 是 的平分线, 是射线 上一点, .动点 从点 出发,以 的速度沿 水平向左作匀速运动,与此同时,动点 从点 出发,也以 的速度沿 竖直向上作匀速运动.连接 ,交 于点 .经过 、 、 三点作圆,交 于点 ,连接 、 .设运动时间为 ,其中 .
(1)求 的值;
(2)是否存在实数 ,使得线段 的长度最大?若存在,求出 的值;若不存在,说明理由.
(3)求四边形 的面积.
已知一次函数y=2x-k与反比例函数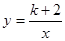 的图像相交于A和B两点.,如果有一个交点A的横坐标为3,
的图像相交于A和B两点.,如果有一个交点A的横坐标为3,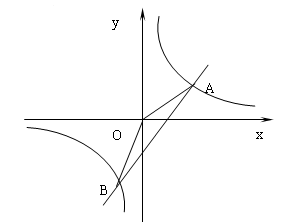
(1)求k的值;
(2)求A、B两点的坐标;
(3)根据图象写出一次函数的值大于反比例函数的值的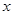 的取值范围
的取值范围
(4)求△AOB的面积;
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标(4,2),过点D(0,3)和E(6,0)的直线分别于AB,BC交于点M,N.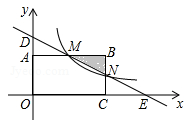
(1)求直线DE的解析式和点M的坐标;
(2)若反比例函数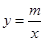 (x>0)的图象经过点M,求该反比函数的解析式,并通过计算判断点N是否在该函数的图象上.
(x>0)的图象经过点M,求该反比函数的解析式,并通过计算判断点N是否在该函数的图象上.
试题篮
()