初中数学相似多边形的性质选择题

如图，梯形ABCD中AD//BC，对角线AC、BD相交于点O，若AO∶CO＝2:3，AD＝4，则BC等于：【   】

A．12           B．8            C．7            D．6

如图，身高1．6m的学生想测量学校旗杆的高度，当他站在C处时，他头顶端的影子正好与旗杆顶端的影子重合，并测得AC=2．0m，BC=8．0m，则旗杆的高度是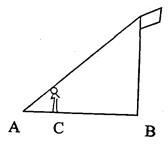

A．6．4m

B．7．0m

C．8．0m

D．9．0m

如图，△A₁B₁C₁是由△ABC沿BC方向平移了BC长度的一半得到的，若△ABC的面积为20 cm²，则四边形A₁DCC₁的面积为（     ）

A．10 cm^2

B．12 cm^2

C．15 cm^2

D．17 cm^2

在等腰△ABC和等腰△DEF中，∠A与∠D是顶角，下列判断正确的是（  ）
①∠A=∠D时，两三角形相似；     ②∠A=∠E时，两三角形相似；
③时，两三角形相似；     ④∠B=∠E时，两三角形相似。

A．1个

B．2个

C．3个

D．4个

如果把三角形的三边按一定的比例扩大，则下列说法正确的是

A．三角形的形状不变，三边的比变大	B．三角形的形状变，三边的比变大
C．三角形的形状变，三边的比不变	D．三角形的形状不变，三边的比不变

如图，E（-4，2），F（-1，-1），以O为位似中心，按比例尺1：2，把△EOF缩小，则点E的对应点E′的坐标为（      ）．

A．（2，-1）或（-2，1）

B．（8，-4）或（-8，4）

C．（2，-1）

D．（8，-4）

如图,斜靠在墙上的梯子AB,梯脚B距墙面1．6米,梯上一点D距墙面1．4米,BD长0．55米,则梯子AB的长为(  )米

A．3．85;

B． 4．00;

C．4．4;

D．4．50．

相距125千米的两地在地图上的距离为25cm,则该地图的比例尺为(  )

A．1∶5000;

B．1∶50000;

C．1∶500000;

D．1∶5000000．

在△ABC和△A₁B₁C₁中，有下列条件：①② ③∠A=∠A₁④∠B=∠B₁⑤∠C=∠C₁，如果从中任取两个条件组成一组，那么能判断△ABC∽△A₁B₁C₁的有(    )

A．4组

B．5组

C．6组

D．7组

如图，AB是斜靠在墙壁上的长梯，梯脚B距墙1.6米，梯上D距离1.4米,BD长0.55米，则梯子的长为(    )

A．3.85米

B．4.00米

C．4.40米

D．4.50米

按如下方法，将△ABC的三边缩小的原来的一半，如图，任取一点O，连AO、BO、CO，并取它们的中点D、E、F，得△DEF，则下列说法正确的个数是（   ）
①△ABC与△DEF是位似图形     ②△ABC与△DEF是相似图形
③△ABC与△DEF的周长比为1:2  ④△ABC与△DEF的面积比为4:1
A．1         B．2         C．3        D．4

下列四个三角形，与右图中的三角形相似的是（  ）
 

如图是圆桌正上方的灯泡O发出的光线照射桌面后，在地面上形成阴影(圆形)的示意图.已知桌面的直径为1.2m，桌面距离地面1m，若灯泡O距离地面3m，则地面上阴影部分的面积为（    ）

A．0.36πm^2

B．0.81πm^2

C．2πm^2

D．3.24πm^2

如图，阳光通过窗口照到室内，在地面上留下1.6m宽的亮区DE，已知亮区一边到窗下的墙脚距离CE=3.6m，窗高AB=1.2m，那么窗口底边离地面的高度BC=          m ．

两个相似三角形的相似比为2 ：3，面积差为30cm²，则较小三角形的面积为         cm²．