如图，已知抛物线y=ax2+bx+c（a≠0）经过A（﹣1，0），B（4，0），C（0，2）三点
（1）求这条抛物线的解析式；
（2）E为抛物线上一动点，是否存在点E使以A、B、E为顶点的三角形与△COB相似？若存在，试求出点E的坐标；若不存在，请说明理由；
如图，在平面直角坐标系中，点A（10，0），以OA为直径在第一象限内作半圆C，点B是该半圆周上一动点，连接OB、AB，并延长AB至点D，使DB=AB，过点D作x轴垂线，分别交x轴、直线OB于点E、F，点E为垂足，连接CF．当∠AOB=30°时，求弧AB的长度；
当DE=8时，求线段EF的长；
在点B运动过程中，是否存在以点E、C、F为顶点的三角形与△AOB相似？若存在，请求出此时点E的坐标；若不存在，请说明理由．
如图，在边长为1的正方形网格中，有一格点△ABC，已知A、B、C三点的坐标分别是A（1，0）B（2，－1）C（3，1）．
（1）请在网格图形中画出平面直角坐标系；
（2）以原点O为位似中心，将△ABC放大2倍，画出放大后的△A′B′C′；
（3）写出△A′B′C′各顶点的坐标：A′____，B′____，C′ ___；
如图，两颗树的高度分别为AB＝6m，CD＝8m，两树的根部间的距离AC＝4m，小强沿着 正对这两棵树的方向从左向右前进，如果小强的眼睛与地面的距离为1.6m，当小强与树AB的距离小于多少时，就不能看到树CD的树顶D？
图，△ABC中，点E、P在边AB上，且AE＝BP，过点E、P作BC的平行线，分别交AC于点F、Q．记△AEF的面积为S1，四边形EFQP的面积为S2，四边形PQCB的面积为S3
（1）求证：EF＋PQ＝BC
（2）若S1＋S3＝S2，求
的值
将△ABC绕点A按逆时针方向旋转θ度，并使各边长变为原来的n倍，得△AB′C′，即如图①，我们将这种变换记为[θ，n]．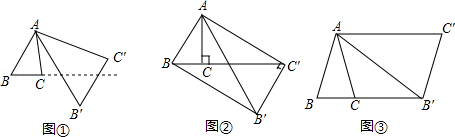
（1）如图①，对△ABC作变换[50°，
]得△AB′C′，则S△AB′C′：S△ABC= ；直线BC与直线B′C′所夹的锐角为 度；
（2）如图②，△ABC中，∠BAC=30°，∠ACB=90°，对△ABC 作变换[θ，n]得△AB'C'，使点B、C、C′在同一直线上，且四边形ABB'C'为矩形，求θ和n的值；
（3）如图③，△ABC中，AB=AC，∠BAC=36°，BC=l，对△ABC作变换[θ，n]得△AB′C′，使点B、C、B′在同一直线上，且四边形ABB'C'为平行四边形，求θ和n的值．
（本题6分）已知：如图，AB和DE是直立在地面上的两根立柱，AB=5m，某一时刻，AB在阳光下的投影BC=4m。
（1）请你在图中画出此时DE在阳光下的投影；（不写做法）
（2）在测量AB的投影长时，同时测出DE在阳光下的投影长为6m，请你计算DE的长。
（本小题8分）已知：如图，△ABC中，∠BAC＝90°，AB＝AC＝1，点D是BC边上的一个动点（不与B，C点重合），∠ADE＝45°．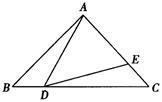
（1）求证：△ABD∽△DCE；
（2）设BD＝x，AE＝y，求y关于x的函数关系式；
（3）当△ADE是等腰三角形时，求AE的长．
如图，⊙O的直径AB＝10，CD是⊙O的弦，AC与BD相交于点P．
(1) 设∠BPC＝α，如果sinα是方程5x2－13x＋6＝0的根,求cosα的值；
(2) 在(1)的条件下，求弦CD的长．
如图，在等腰Rt△ABC中，∠C=90°，正方形DEFG的顶点D在边AC上，点E，F在边AB上，点G在边BC上．
⑴求证：△ADE≌△BGF；
⑵若正方形DEFG的面积为16，求AC的长．
（本题9分）如图，在□ABCD中，过点B作BE⊥CD于E，F为AE上一点，且∠BFE＝∠C．
（1）求证：△ABF∽△EAD；
（2）若AB＝4，∠BAE＝30º，求AE的长；
（3）在（1）（2）的条件下，若AD＝3，求BF的长．
已知：如图ΔABC中，D、E、F分别是AB、AC、BC的中点.
（1）若AB=10cm，AC=6cm,则四边形ADFE的周长为______cm
（2）若ΔABC周长为6cm,面积为12cm2,则ΔDEF的周长是 _____,面积是_____
试题篮
()
粤公网安备 44130202000953号
是∠ABC的角平分线，求证：
∽
．
,猜想EF与DE的位置关系,并说明理由.
