初中数学相似多边形的性质解答题

如图，已知AB是⊙O的直径，AB=8， 点C在半径OA上（点C与点O、A不重合），过点C作AB的垂线交⊙O于点D，连结OD，过点B作OD的平行线交⊙O于点E、交射线CD于点F．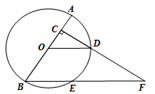

（1）若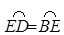，求∠F的度数；
（2）设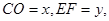写出与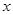之间的函数解析式，并写出自变量取值范围；
（3）设点C关于直线OD的对称点为P，若△PBE为等腰三角形，求OC的长．

已知：如图，在等腰直角△ABC中，AC=BC，斜边AB的长为4，过点C作射线CP//AB，D为射线CP上一点，E在边BC上（不与B、C重合），且∠DAE=45°，AC与DE交于点O．

（1）求证：△ADE∽△ACB；
（2）设CD=x，BAE = y，求y关于x的函数解析式，并写出它的定义域；
（3）如果△COD与△BEA相似，求CD的值．

（本小题满分10分）如图1，△ABC是等腰直角三角形，四边形ADEF是正方形，D、F分别在AB、AC边上，此时BD=CF，BD⊥CF成立．

（1）当正方形ADEF绕点A逆时针旋转θ（0°＜θ＜90°）时，如图2，BD=CF成立吗？若成立，请证明；若不成立，请说明理由．
（2）当正方形ADEF绕点A逆时针旋转45°时，如图3，延长BD交CF于点G．求证：BD⊥CF；
（3）在（2）小题的条件下, AC与BG的交点为M， 当AB=4，AD= 时，求线段CM的长．

如图，已知抛物线与x轴交于A（－1，0）、E（3，0）两点，与y轴交于点B（0，3）。

（1）求抛物线的解析式；
（2）设抛物线顶点为D，求四边形AEDB的面积；
（3）△AOB与△DBE是否相似？如果相似，请给以证明；如果不相似，请说明理由。

如图，已知抛物线与x轴交于A、B两点，点C是抛物线在第一象限内部分的一个动点，点D是OC的中点，连接BD并延长，交AC于点E.

（1）说明：；
（2）当点C、点A到y轴距离相等时，求点E坐标.
（3）当的面积为时，求的值.

如图1，将三角板放在正方形ABCD上，使三角板的直角顶点E与正方形ABCD的顶点A重合．三角板的一边交CD于点F，另一边交CB的延长线于点G．

（1）求证：EF＝EG；
（2）如图2，移动三角板，使顶点E始终在正方形ABCD的对角线AC上，其他条件不变，（1）中的结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由；
（3）如图3，将（2）中的“正方形ABCD”改为“矩形ABCD”，且使三角板的一边经过点B，其他条件不变，若AB＝a，BC＝b，请直接写出的值．

如图，在矩形ABCD中，AB=4，AD=5，P是射线BC上的一个动点，过点P作PE⊥AP，交射线DC于点E，射线AE交射线BC于点F，设BP=a．

（1）当点P在线段BC上时（点P与点B，C都不重合），试用含a的代数式表示CE；
（2）当a=3时，连结DF，试判断四边形APFD的形状，并说明理由；
（3）当tan∠PAE=时，求a的值．

（本小题满分１4分）如图，在平面直角坐标系中，抛物线过点（0，4）和（8，0），P（t，0）是轴正半轴上的一个动点，M是线段AP的中点，将线段MP绕点P顺时针旋转90°得线段PB．过点B作轴的垂线、过点A作轴的垂线，两直线相交于点D．

（1）求此抛物线的对称轴；
（2）当为何值时，点D落在抛物线上？
（3）是否存在，使得以A、B、D为顶点的三角形与△PEB相似？若存在，求此时的值；若不存在，请说明理由．

已知，如图，以点P（﹣1，0）为圆心的圆，交x轴于A、C两点（A在C的左侧），交y轴于B、D两点（B在D的上方），且∠BAC＝30°，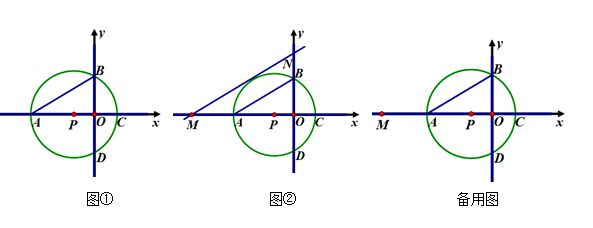

（1）如图①求⊙P的半径及点B的坐标；
（2）点Q是⊙P上任意一点，求△ABQ面积S的取值范围；
（3）如图②，已知点M（－5，0），过M作直线y=kx+b交y轴于点N，
①若MN//AB，试判断MN与⊙P的位置关系，并说明理由；
②在该直线上存在一点G，使以G、A、C为顶点的三角形是直角三角形，且满足条件的点G有且只有三个不同位置，求直线MN的函数关系式．

如图，在△ABC中，∠B=90°，∠ACB=60°，AB=，AD⊥AC，连接CD.点E在AC上，，过点E作MN⊥AC，分别交AB、CD于点M、N.

（1）求ME的长；
（2）当AD=3时，求四边形ADNE的周长.

如图，Rt△ABC中，∠ACB=90°，AC=4，BC=3，P是斜边AB上的一个动点（点P与点A、B不重合），以点P为圆心，PA为半径的⊙P与射线AC的另一个交点为D，射线PD交射线BC于点E．
（1）如图1，若点E在线段BC的延长线上，设AP=x，CE=y，

①求y关于x的函数关系式，并写出x的取值范围；
②当以BE为直径的圆和⊙P外切时，求AP的长；
（2）设线段BE的中点为Q，射线PQ与⊙P相交于点I，若CI=AP，求AP的长．

如图，在□ABCD中，E是AB的中点，ED和AC相交于点F，过点F作FG∥AB，交AD于点G．

（1）求证：AB=3FG；
（2）若AB:AC=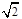: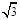，求证：．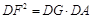

在△ABC中，∠A＝90°，AB＝8，AC＝6，M是AB上的动点（不与A，B重合），过M点作MN∥BC交AC于点N．以MN为直径作⊙O，并在⊙O内作内接矩形AMPN．设AM＝．

（1）用含的代数式表示△MNP的面积S；
（2）在动点M的运动过程中，记△MNP与梯形BCNM重合部分的面积为，试求关于的函数表达式，并求为何值时，的值最大，最大值是多少？

如图，已知抛物线与轴相交于A、B两点，与轴相交于点C，若已知B点的坐标为B（8，0）.

（1）求抛物线的解析式及其对称轴方程；
（2）连接AC、BC，试判断△AOC与△COB是否相似？并说明理由；
（3）M为抛物线上BC之间的一点，N为线段BC上的一点，若MN∥轴，求MN的最大值；
（4）在抛物线的对称轴上是否存在点Q，使△ACQ为等腰三角形？若存在，求出符合条件的Q点坐标；若不存在，请说明理由.

如图，点是菱形的对角线上一点，连接并延长，交于，交的延长线于点．

（1）图中△与哪个三角形全等？并说明理由.
（2）求证：△∽△.
（3）猜想：线段，，之间存在什么关系？并说明理由．