初中数学相似多边形的性质解答题

如图，斜坡AC的坡度（坡比）为1:，AC＝10米．坡顶有
一旗杆BC，旗杆顶端B点与A点有一条彩带AB相连，AB＝14米．试求旗杆BC的高度．

如图，边长为4的正方形OABC的顶点O为坐标原点，点A
在x轴的正半轴上，点C在y轴的正半轴上．动点D在线段BC上移动（不与B，C重合），
连接OD，过点D作DE⊥OD，交边AB于点E，连接OE。
（1）当CD=1时，求点E的坐标；
（2）如果设CD=t，梯形COEB的面积为S，那么是否存在S的最大值？若存在，请求出这
个最大值及此时t的值；若不存在，请说明理由。

如图（1），（2）所示，矩形ABCD的边长AB=6，BC=4，点F在DC上，DF=2。
动点M、N分别从点D、B同时出发，沿射线DA、线段BA向点A的方向运动（点M可
运动到DA的延长线上），当动点N运动到点A时，M、N两点同时停止运动。连接FM、
FN，当F、N、M不在同一直线时，可得△FMN，过△FMN三边的中点作△PQW。设动点
M、N的速度都是1个单位/秒，M、N运动的时间为x秒。试解答下列问题：
（1）说明△FMN∽△QWP；
（2）设0≤x≤4（即M从D到A运动的时间段）。试问x为何值时，△PQW为直角三角形？
当x在何范围时，△PQW不为直角三角形？
（3）问当x为何值时，线段MN最短？求此时MN的值。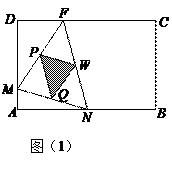
            

(本题满分10分)如图，在平面直角坐标系中，把抛物线向左平移1个单位，再向下平移4个单位，得到抛物线.所得抛物线与轴交于两点（点在点的左边），与轴交于点，顶点为.
（1）写出的值；
（2）判断的形状，并说明理由；
（3）在线段上是否存在点，使∽？若存在，求出点的坐标；若不存在，说明理由.

（本小题满分12分）
如图，一块直角三角板的直角顶点P放在正方形ABCD的BC边上，并且使一条直角边经过点D，另一条直角边与AB交于点Q.
⑴ 请你写出一对相似三角形，并加以证明；
⑵ 当点P满足什么条件时， ，请证明你的结论；

(8分) 甲、乙、丙三个学习小组于同一时刻在阳光下对校园中一些物体进行了测量.下面是他们通过测量得到的一些信息：
甲组：如图(1)，测得一根直立于平地，长为80cm的竹竿的影长为60cm.
乙组：如图(2)，测得学校旗杆的影长为900cm.
丙组：如图(3)，测得校园景灯（灯罩视为圆柱体，灯杆粗细忽略不计）的灯罩部分影长HQ
为90cm，灯杆被阳光照射到的部分PG长40cm，未被照射到的部分KP长24cm。
（1）请根据甲、乙两组得到的信息计算出学校旗杆的高度；
（2）请根据甲、丙两组得到的信息，求：
①灯罩底面半径MK的长；
②灯罩的主视图面积。

如图1，在四边形ABCD的AB边上任取一点E（点E不与点A、点B
重合），分别连接ED、EC，可以把四边形ABCD分成3个三角形．如果其中有2个三角形
相似，我们就把点E叫做四边形ABCD的AB边上的相似点；如果这3个三角形都相似，
我们就把点E叫做四边形ABCD的AB边上的强相似点．

（1）若图1中，∠A＝∠B＝∠DEC＝50°，说明点E是四边形ABCD的AB边上的相似点；
（2）①如图2，画出矩形ABCD的AB边上的一个强相似点．（要求：画图工具不限，不写画法，保留画图痕迹或有必要的说明．）
②对于任意的一个矩形，是否一定存在强相似点？如果一定存在，请说明理由；如果不一定存在，请举出反例．
（3）在梯形ABCD中，AD∥BC，AD＜BC，∠B＝90°，点E是梯形ABCD的AB边上的一个强相似点，判断AE与BE的数量关系并说明理由．

如图，在Rt△ABC中，∠C=90°，AC=BC=4cm，点D为AC边上一
点，且AD=3cm，动点E从点A出发，以1cm/s的速度沿线段AB向终点B运动，运动
时间为x s．作∠DEF=45°，与边BC相交于点F．设BF长为ycm．
（1）当x=   ▲ s时，DE⊥AB；
（2）求在点E运动过程中，y与x之间的函数关系式及点F运动路线的长；
（3）当△BEF为等腰三角形时，求x的值．

在边长为1的正方形网格中，正方形与正方形的位置如图所示．
（1）请你按下列要求画图：
① 联结交于点；
② 在上取一点，联结，，使△与△相似；
（2）若是线段上一点，连结并延长交四边形的一边于点，且满足，则的值为_____________．

如图，在中，，是角平分线，平分交于
点，经过两点的交于点，交于点，恰为的直径．

（1）求证：与相切；
（2）当时，求的半径．

如图,设抛物线C₁:, C₂:,C₁与C₂的交点为A,
B,点A的坐标是,点B的横坐标是－2.
（1）求的值及点B的坐标； 
（2）点D在线段AB上,过D作x轴的垂线,垂足为点H,在DH的右侧作正三角形DHG. 过C₂顶点Ｍ的直线记为,且与x轴交于点N.
①若过△DHG的顶点G,点D的坐标为(1, 2)，求点N的横坐标；
②若与△DHG的边DG相交,求点N的横坐标的取值范围.

等腰△ABC，AB=AC=８，∠BAC=120°，P为BC的中点，小亮拿着30⁰角的透明三角板，使30⁰角的顶点落在点P，三角板绕P点旋转．
（1）如图a，当三角板的两边分别交AB、AC于点E、F时．求证：△BPE∽△CFP；
（2）操作：将三角板绕点P旋转到图b情形时，三角板的两边分别交BA的延长线、边AC于点E、F．
①探究１：△BPE与△CFP还相似吗？
②探究２：连结EF，△BPE与△PFE是否相似？请说明理由；
③设EF=m，△EPF的面积为S，试用m的代数式表示S．
   

梯形ABCD中，AD∥BC，BC=20cm，AD=10cm，现有两个动点P、Q分别从B、D两点同时出发，点P以每秒2cm的速度沿BC向终点C移动，点Q以每秒1cm的速度沿DA向终点A移动，线段PQ与BD相交于点E，过E作EF∥BC交CD于点F，射线QF交BC的延长线于点H，设动点P、Q移动的时间为t（单位：秒，0＜t＜10）．
（1）当t为何值时，四边形PCDQ为平行四边形？
（2）在P、Q移动的过程中，线段PH的长是否发生改变？如果不变，求出线段PH的长；如果改变，请说明理由．

如图，已知AB=AC，∠A=36°，AB的中垂线MD交AC于点D、交AB于点M．下列结论：
①BD是∠ABC的平分线；
②△BCD是等腰三角形；
③△ABC∽△BCD；
④△AMD≌△BCD．
正确的有（　　）个．

A、4        B、3        C、2        D、1

（本题满分12分，第（1）、（2）题各6分）
如图，已知抛物线y＝ax²＋bx＋c与x轴交于A、B两点，与y轴交于点C， D为OC的中点，直线AD交抛物线于点E（2，6），且△ABE与△ABC的面积之比为3∶2．
（1）求直线AD和抛物线的解析式；
（2）抛物线的对称轴与轴相交于点F，点Q为直线AD上一点，且△ABQ与△ADF相似，直接写出点Q点的坐标．