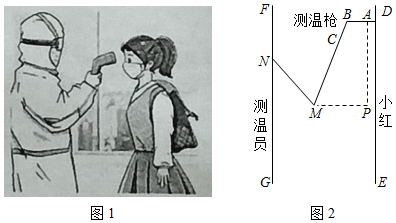
图1是疫情期间测温员用"额温枪"对小红测温时的实景图,图2是其侧面示意图,其中枪柄 与手臂 始终在同一直线上,枪身 与额头保持垂直.量得胳膊 , ,肘关节 与枪身端点 之间的水平宽度为 (即 的长度),枪身 .
(1)求 的度数;
(2)测温时规定枪身端点 与额头距离范围为 .在图2中,若测得 ,小红与测温员之间距离为 .问此时枪身端点 与小红额头的距离是否在规定范围内?并说明理由.(结果保留小数点后一位)
(参考数据: , , ,
某种落地灯如图1所示, 为立杆,其高为 ; 为支杆,它可绕点 旋转,其中 长为 ; 为悬杆,滑动悬杆可调节 的长度.支杆 与悬杆 之间的夹角 为 .
(1)如图2,当支杆 与地面垂直,且 的长为 时,求灯泡悬挂点 距离地面的高度;
(2)在图2所示的状态下,将支杆 绕点 顺时针旋转 ,同时调节 的长(如图 ,此时测得灯泡悬挂点 到地面的距离为 ,求 的长.(结果精确到 ,参考数据: , , , , ,

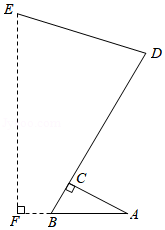
如图,为了测量河对岸两点 , 之间的距离,在河岸这边取点 , .测得 , , , , .设 , , , 在同一平面内,求 , 两点之间的距离.
(参考数据: , .

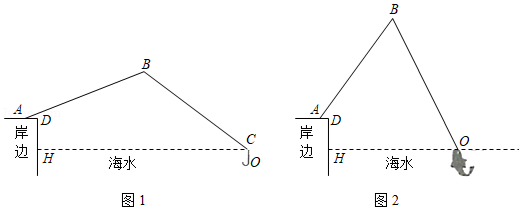
我市的前三岛是众多海钓人的梦想之地.小明的爸爸周末去前三岛钓鱼,将鱼竿 摆成如图1所示.已知 ,鱼竿尾端 离岸边 ,即 .海面与地面 平行且相距 ,即 .
(1)如图1,在无鱼上钩时,海面上方的鱼线 与海面 的夹角 ,海面下方的鱼线 与海面 垂直,鱼竿 与地面 的夹角 .求点 到岸边 的距离;
(2)如图2,在有鱼上钩时,鱼竿与地面的夹角 ,此时鱼线被拉直,鱼线 ,点 恰好位于海面.求点 到岸边 的距离.
(参考数据: , , , , ,
某限高曲臂道路闸口如图所示, 垂直地面 于点 , 与水平线 的夹角为 , ,若 米, 米,车辆的高度为 (单位:米),不考虑闸口与车辆的宽度:
①当 时, 小于3.3米的车辆均可以通过该闸口;
②当 时, 等于2.9米的车辆不可以通过该闸口;
③当 时, 等于3.1米的车辆不可以通过该闸口.
则上述说法正确的个数为

| A. |
0个 |
B. |
1个 |
C. |
2个 |
D. |
3个 |
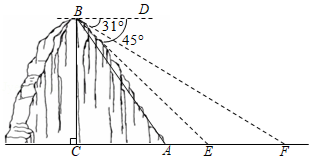
某镇为创建特色小镇,助力乡村振兴,决定在辖区的一条河上修建一座步行观光桥.如图,该河旁有一座小山,山高 ,坡面 的坡度 (注:坡度 是指坡面的铅直高度与水平宽度的比),点 、 与河岸 、 在同一水平线上,从山顶 处测得河岸 和对岸 的俯角分别为 , .
(1)求山脚 到河岸 的距离;
(2)若在此处建桥,试求河宽 的长度.(结果精确到
(参考数据: , ,
已知锐角 中,角 、 、 的对边分别为 、 、 ,边角总满足关系式: .

(1)如图1,若 , , ,求 的值;
(2)某公园准备在园内一个锐角三角形水池 中建一座小型景观桥 (如图2所示),若 , 米, 米, ,求景观桥 的长度.
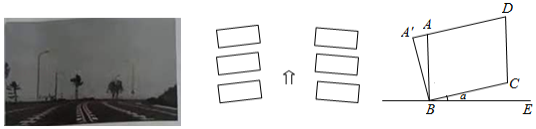
高速公路上有一种标线叫纵向减速标线,外号叫鱼骨线,作用是为了提醒驾驶员在开车时减速慢行.如图,用平行四边形 表示一个"鱼骨", 平行于车辆前行方向, , ,过 作 的垂线,垂足为 点的视觉错觉点),若 , ,则 .
如图是某商场营业大厅自动扶梯的示意图.自动扶梯 的倾斜角为 ,大厅两层之间的距离 为6米,则自动扶梯 的长约为 , ,

| A. |
7.5米 |
B. |
8米 |
C. |
9米 |
D. |
10米 |
如图,某梯子长10米,斜靠在竖直的墙面上,当梯子与水平地面所成角为 时,梯子顶端靠在墙面上的点 处,底端落在水平地面的点 处,现将梯子底端向墙面靠近,使梯子与地面所成角为 ,已知 ,则梯子顶端上升了

| A. |
1米 |
B. |
1.5米 |
C. |
2米 |
D. |
2.5米 |
一种可折叠的医疗器械放置在水平地面上,这种医疗器械的侧面结构如图实线所示,底座为 ,点 、 、 在同一条直线上,测得 , , , ,其中一段支撑杆 ,另一段支撑杆 .求支撑杆上的点 到水平地面的距离 是多少?(用四舍五入法对结果取整数,参考数据: , , ,
如图,点 为正六边形 对角线 上一点, , ,则 的值是

| A. |
20 |
B. |
30 |
| C. |
40 |
D. |
随点 位置而变化 |
如图1是平凉市地标建筑“大明宝塔”,始建于明嘉靖十四年 年),是明代平凉韩王府延恩寺的主体建筑.宝塔建造工艺精湛,与崆峒山的凌空塔遥相呼应,被誉为平凉古塔“双璧”.某数学兴趣小组开展了测量“大明宝塔的高度”的实践活动,具体过程如下:
方案设计:如图2,宝塔 垂直于地面,在地面上选取 , 两处分别测得 和 的度数 , , 在同一条直线上).
数据收集:通过实地测量:地面上 , 两点的距离为 , , .
问题解决:求宝塔 的高度(结果保留一位小数).
参考数据: , , , , , .
根据上述方案及数据,请你完成求解过程.

试题篮
()