初中数学对称式和轮换对称式试题

已知点P（a，2a+3）点在第二、四象限的角平分线上，则a=  ．

已知点A（a，-2）与点B（3，-2）关于y轴对称，则a=             ．

在平面直角坐标系中，P点关于原点的对称点为P₁（-3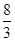，-），P点关于x轴的对称点为P₂（a，b），则=（ ）

A．-2

B．2

C．4

D．-4

如图，在平面直角坐标系中，点B、C、E、在y轴上，Rt△ABC经过变换得到Rt△ODE．若点C的坐标为（0，1），AC=2，则这种变换可以是（ ）

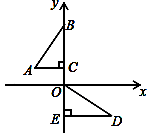
A．△ABC绕点C顺时针旋转90°，再向下平移3个单位
B．△ABC绕点C顺时针旋转90°，再向下平移1个单位
C．△ABC绕点C逆时针旋转90°，再向下平移1个单位
D．△ABC绕点C逆时针旋转90°，再向下平移3个单位

如图，在平面直角坐标系中，△ABC和△A₁B₁C₁关于点E成中心对称．

（1）画出对称中心E，并写出点E、A、C的坐标；
（2）P（a，b）是△ABC的边AC上一点，△ABC经平移后点P的对应点为P₂（a+6，b+2），请画出上述平移后的△A₂B₂C₂，并写出点A₂、C₂的坐标；
（3）判断△A₂B₂C₂和△A₁B₁C₁的位置关系（直接写出结果）．

如图，直角梯形ABCD中，AD∥BC，AB⊥BC，AD=2，BC=3，∠BCD=45°，将腰CD以点D为中心逆时针旋转90°至ED，连结AE，CE，则△ADE的面积是_____．

长方形ABCD中，AD="4" cm，AB="10" cm，按右图方式折叠，使点B与点D重合，折痕是EF，则DE等于          （   ）

A．4．2 cm

B．5．8 cm

C．4．2 cm或5．8 cm

D．6 cm

在如图所示的直角坐标系中，每个小方格都是边长为1的正方形，△ABC的顶点均在格点上，点A的坐标是（－3，－1）．

（1）将△ABC沿y轴正方向平移3个单位得到△A₁B₁C₁，画出△A₁B₁C₁，并写出点B₁坐标；
（2）画出△A₁B₁C₁关于y轴对称的△A₂B₂C₂，并写出点C₂的坐标．

在平面直角坐标系中，点A的坐标是（0，3），点B的坐标是（-4，0），
（1）若将△AOB绕点O逆时针旋转90°得到，请在图中画出，并写出点的坐标；
（2）若将△AOB绕点A逆时针旋转90°得到△AEF，点O，B对应点分别是E，F． 请在图中画出△AEF，并写出点E，F的坐标．

如图，在△ABC中，∠CAB=65°，将△ABC在平面内绕点A逆时针旋转到△AB′C′的位置，使CC′∥AB，则旋转角的度数为（     ）
 

A．35°

B．40°

C．50°

D．65°

在△ABC中，∠CAB=75°，在同一平面内，将△ABC绕点A逆时针旋转到△AED的位置，使得DE∥AB，则∠DAB等于      ．

下列电视台的台标，是中心对称图形的是（ ）

A．

B．

C．

D．

已知：图中点A，点B的坐标分别为（﹣2，1）和（2，3）．

（1）在图（1）中分别画出线段AB关于x轴和y轴的对称线段A₁B₁及A₂B₂；
（2）在图（2）中分别画出线段AB关于直线x=﹣1和直线y=4的对称线段A₃B₃及A₄B₄；
（3）写出点A₃、B₃与点A₄、B₄的坐标．

如图，动点P从（0，3）出发，沿所示方向运动，每当碰到长方形OABC的边时反弹，反弹时反射角等于入射角，当点P第2013次碰到矩形的边时，点P的坐标为（   ）

A．（1，4）

B．（5，0）

C．（6，4）

D．（8，3）

如图，在平面直角坐标系中，Rt△ABC的三个顶点分别是A（－3，2），B（0，4），C（0，2）．
A₁
（1）画出△ABC关于x轴对称的△A₁B₁C₁；
（2）移△ABC，若A的对应点的坐标为（0，4），画出平移后对应的△；
（3）在轴上有一点P，使得PA+PB的值最小，请直接写出点P的坐标．