初中数学对称式和轮换对称式解答题

图①、图②均为7×6的正方形网格，点A、B、C在格点上．

（1）在图①中确定格点D，并画出以A、B、C、D为顶点的四边形， 使其为轴对称图形．（画一个即可）
（2）在图②中确定格点E，并画出以A、B、C、E为顶点的四边形，使其为中心对称图形．（画一个即可）

（7分) 如图，平面直角坐标系中，已知点A（－3，3），B（－5，1），C（－2，0），P()是△ABC的边AC上任意一点，△ABC经过平移后得到△A₁B₁C₁，已知点P的对应点为P₁()．

（1）直接写出点C₁的坐标；
（2）在图中画出△A₁B₁C₁；
（3）求△AOA₁的面积．

如图1，两个不全等的等腰直角三角形和叠放在一起，并且有公共的直角顶点．

（1）在图1中，你发现线段，的数量关系是     ，直线，相交成     度角．
（2）将图1中的绕点顺时针旋转角，连结AC、BD得到图2，这时（1）中的两个结论是否成立？请作出判断并说明理由．
（3）将图1中的绕点顺时针旋转一个锐角，连结AC、BD得到图3，这时（1）中的两个结论是否成立？请作出判断并说明理由．

如图所示，在△OAB中，点B的坐标是（0，4），点A的坐标是（3，1）．

（1）画出△OAB向下平移4个单位长度、再向左平移2个单位长度后的△O₁A₁B₁．
（2）画出△OAB绕点O逆时针旋转90°后的△OA₂B₂，并求出点A旋转到A₂所经过的路径长（结果保留π）．

如图，在平面直角坐标系中，已知△AOB是等边三角形,点A的坐标是（0，3），点B在第一象限，点P是x轴上的一个动点，连结AP，并把△AOP绕着点A按逆时针方向旋转，使边AO与AB重合，得到△ABD．当点P运动到点（,0）时，求此时DP的长及点D的坐标。

△ABC在平面直角坐标系中的位置如图所示，点O为坐标原点：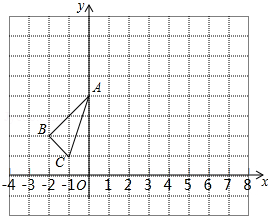

（1）作出△ABC关于y轴对称的△A₁B₁C₁；
（2）将△ABC向右平移6个单位，作出平移后的对应△A2B2C2，并画出△A₁B₁C₁与△A₂B₂C₂，的对称轴；
（3）（2）中△ABC向右平移个单位时，OA₂+OB₂的值最小．

在如图所示的网格图中．每个小正方形的边长均为1个单位，又在Rt△中，，

（1）试在图中作出△以为旋转中心，沿顺时针方向旋转90°后的图形△；
（2）若点的坐标为（－3，5），试在图中画出直角坐标系，并写出的坐标；
（3）在上述坐标系中作出△关于原点对称的图形△，写出的坐标．

如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC（顶点是网格线的交点）．

（1）将△ABC绕点B顺时针旋转90°得到△A′BC′，请画出△A′BC′；
（2）求BA边旋转到B A′位置时所扫过图形的面积．

（本小题满分8分）如图，正方形网格中的每个小正方形边长都是1．
（利用网格线进行画图，别忘了标上字母噢！）

（1） 在图1中，画一个顶点为格点、面积为5的正方形；
（2） 在图2中，已知线段AB、CD，画线段EF，使它与AB、CD组成轴对称图形；
（要求画出所有符合题意的线段）
（3） 在图3中，找一格点D，满足：①到CB、CA的距离相等；②到点A、C的距离相等．

如图，直角坐标系中，△ABC的顶点都在网格点上，其中，C点坐标为（1，2）．

（1）写出点A、B的坐标：
（2）将△ABC先向左平移2个单位长度，再向上平移1个单位长度，得到△A′B′C′，则A′B′C′的三个顶点坐标分别是A′（，）、B′（，）、C′（，）．
（3）△ABC的面积为    ．

在△ABC中，∠C=90°，AC=6，BC=8，DE垂直平分AB，求BE的长．

在数学兴趣小组活动中，小明进行数学探究活动，将边长为2的正方形ABCD与边长为2的正方形AEFG按图1位置放置，AD与AE在同一直线上，AB与AG在同一直线上．
（1）小明发现DG⊥BE，请你帮他说明理由．
（2）如图2，小明将正方形ABCD绕点A逆时针旋转，当点B恰好落在线段DG上时，请你帮他求出此时BE的长．
（3）如图3，小明将正方形ABCD绕点A继续逆时针旋转，线段DG与线段BE将相交，交点为H，写出△GHE与△BHD面积之和的最大值，并简要说明理由．

某校九年级学习小组在探究学习过程中，用两块完全相同的且含60°角的直角三角板ABC与AFE按如图（1）所示位置放置放置，现将Rt△AEF绕A点按逆时针方向旋转角α（0°＜α＜90°），如图（2），AE与BC交于点M，AC与EF交于点N，BC与EF交于点P．

（1）求证：AM=AN；
（2）当旋转角α=30°时，四边形ABPF是什么样的特殊四边形？并说明理由．

如图，△ABC中，AB=AC，∠A=36°，AC的垂直平分线交AB于E，D为垂足，连结EC．

（1）求∠ECD的度数；
（2）若CE=12，求BC长．

问题：如图（1），点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，试判断BE、EF、FD之间的数量关系．
【发现证明】
小聪把△ABE绕点A逆时针旋转90°至△ADG，从而发现EF=BE+FD，请你利用图（1）证明上述结论．
【类比引申】
如图（2），四边形ABCD中，∠BAD≠90°，AB=AD，∠B+∠D=180°，点E、F分别在边BC、CD上，则当∠EAF与∠BAD满足∠BAD=2∠EAF关系时，仍有EF=BE+FD．
【探究应用】
如图（3），在某公园的同一水平面上，四条通道围成四边形ABCD．已知AB=AD=80米，∠B=60°，∠ADC=120°，∠BAD=150°，道路BC、CD上分别有景点E、F，且AE⊥AD，DF=40（﹣1）米，现要在E、F之间修一条笔直道路，求这条道路EF的长（结果取整数，参考数据：=1．41，=1．73）