初中数学二元一次不定方程的应用解答题

每年的6月5日为世界环保日，为提倡低碳环保，某公司决定购买10台节省能源的新机器，现有甲、乙两种型号的新机器可选，其中每台的价格、工作量如下表．

	甲型机器	乙型机器
价格（万元/台）	a	b
产量（吨/月）	240	180

经调查：购买一台甲型机器比购买一台乙型机器多2万元，购买2台甲型机器比购买3台乙型机器少6万元．
（1）求a、b的值；
（2）若该公司购买新机器的资金不能超过110万元，请问该公司有几种购买方案？
（3）在（2）的条件下，若公司要求每月的产量不低于2040吨，请你为该公司设计一种最省钱的购买方案．

小明爸爸骑摩托车带着小明在公路行驶，下图是小明在不同时间看到的里程碑情况.你能确定小明在12：00时看到的里程碑上的数吗？

如果设小明在12:00时看到的数的十位数字是x，个位数字是y，那么
（1）12:00时小明看到的数可表示为                                           ，
根据“两个数字之和是7”，可列出方程                                     ；
（2）13:00时小明看到的数可表示为                                           ，
根据“13:00时看到的两位数比12:00时看到的大45”，可列出方程              ；
（3）根据以上分析，得出方程组，并求出小明在12：00时看到的里程碑上的数.

目前节能灯在城市已基本普及，今年山东省面向县级及农村地区推广，为响应号召，某商场计划购进甲，乙两种节能灯共1200只，这两种节能灯的进价、售价如下表：

	进价（元/只）	售价（元/只）
甲型	25	30
乙型	45	60

 
（1）如何进货，进货款恰好为46000元？
（2）如何进货，商场销售完节能灯时获利最多且不超过进货价的30%，此时利润为多少元？

为落实“促民生、促经济”政策，某公司今年1月份调整了职工的月工资分配方案，调整后月工资由基本保障工资和计件奖励工资两部分组成（计件工资=销售每件产品的奖励金额×销售件数）．下表是甲、乙两位职工今年1月份的工资情况信息：

职工	甲	乙
月销售件数（件）	200	180
月工资（元）	1800	1700

 
（1）试求调整后职工的月基本保障工资和销售每件产品的奖励金额各多少元？
（2）如果职工丙要想在今年二月份月工资达到2600元，那么丙当月应销售多少件产品？

四川地震后，某商家为支援灾区人民，计划捐赠帐篷16800顶，该商家备有2辆大货车、8辆小货车运送帐篷．计划大货车比小货车每辆每次多运帐篷200顶，大、小货车每天均运送一次，两天恰好运完．
（1）求大、小货车原计划每辆每次各运送帐篷多少顶？
（2）因地震导致路基受损，实际运送过程中，每辆大货车每次比原计划少运200m顶，每辆小货车每次比原计划少运300m顶，为了尽快将帐篷运送到灾区，大货车每天比原计划多跑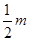次，小货车每天比原计划多跑m次，一天恰好运送了帐篷14400顶，求m的值．

解方程组

(1)有甲、乙、丙三种商品，如果购甲3件、乙2件、丙1件共需15元，如果购甲1件、乙2件、丙3件共需25元，那么购甲、乙、丙各1件共需多少元？
（2）已知2a+b+3c=15，3a+b+5c=25，则a+b+c=               
（3）已知2a+b+xc=15，3a+b+yc=25， 要想求出a+b+c的值，x与y必须满足的关系是？

某公司要把240吨白砂糖运往某市的A、B两地，用大、小两种货车共20辆，恰好能一次性装完这批白砂糖．已知这两种货车的载重量分别为15吨/辆和10吨/辆，运往A地的运费为：大车630元/辆，小车420元/辆；运往B地的运费为：大车750元/辆，小车550元/辆．
（1）求两种货车各用多少辆；
（2）如果安排10辆货车前往A地，其中调往A地的大车有a辆，其余货车前往B地，若设总运费为W，求W与a的关系式（用含有a的代数式表示W）．

小武新家装修，在装修客厅时，购进彩色地砖和单色地砖共100块，共花费5600元．已知彩色地砖的单价是80元/块，单色地砖的单价是40元/块．
（1）两种型号的地砖各采购了多少块？
（2）如果厨房也要铺设这两种型号的地砖共60块，且采购地砖的费用不超过3200元，那么彩色地砖最多能采购多少块？

已知：的立方根是3，16的算术平方根是，求：
（1）、的值；
（2）的平方根．

随着国家“亿万青少年学生阳光体育运动”活动的启动，某市各中小学也开创了体育运动的一个新局面．某校八年级（1）、（2）两个班共有100人，在两个多月的长跑活动之后，学校对这两个班的体能进行了测试，大家惊喜的发现（1）班的合格率为96%，（2）班的合格率为90%，而两个班的总合格率为93%，求八年级（1）、（2）班各有多少人？

请根据图中提供的信息，回答下列问题：

一个水瓶与一个水杯分别是多少元？

某加工厂投资兴建2条全自动生产线和1条半自动生产线共需资金26万元，而投资兴建1条全自动生产线和3条半自动生产线共需资金28万元
（1）求每条全自动生产线和半自动生产线的成本各为多少万元？
（2）据预测，2015年每条全自动生产线的毛利润为26万元，每条半自动生产线的毛利润为16万元.这－年，该加工厂共投资兴建10条生产线，若想获得不少于120万元的纯利润，则2015年该加工厂至少需投资兴建多少条全自动生产线？（纯利润=毛利润－成本）

为响应国家节能减排的号召，鼓励居民节约用电，各省先后出台了居民用电“阶梯价格”制度，如表中是某省的电价标准（每月）．例如：方女士家5月份用电500度，电费=180×0.6+220×二档电价+100×三档电价=352元；李先生家5月份用电460度，交费316元，请问表中二档电价、三档电价各是多少？

某旅馆的客服有三人间和两人间两种，三人间每人每天25元，两人间每人每天35元。一个50
人的旅游团到该旅馆住宿，租住了若干客房，且每个客房正好住满，一天共花去住宿费1510元，两种客房
各租住了多少间？