初中数学二元二次方程组解答题

先化简，再求值：，其中x=+1．

我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”，即已知三角形的三边长，求它的面积．用现代式子表示即为：
 …… ① （其中、、为三角形的三边长，为面积）．而另一个文明古国古希腊也有求三角形面积的海伦公式：
 …… ②（其中）．
（1）若已知三角形的三边长分别为5、7、8，试分别运用公式①和公式②，计算该三角形的面积（结果保留根号）；
（2）你能否由公式①推导出公式②？请试试．

（1）计算：    
（2）先化简，再求值：， 其中x=．

先化简，再求值：，其．

先化简，再求值：，其中．

阅读材料： 小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如：，善于思考的小明进行了以下探索：
设（其中均为整数），则有 ．
∴．这样小明就找到了一种把部分的式子化为平方式的方法．
请你仿照小明的方法探索并解决下列问题：
当均为正整数时，若，用含m、n的式子分别表示，得 ＝　   　，＝　   　；
（2）利用所探索的结论，找一组正整数，填空：   ＋　 　＝(　 　＋　 　)²；
（3）若，且均为正整数，求的值．

观察下列一组等式的化简．然后解答后面的 问题：
；
；
…
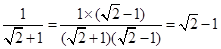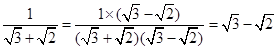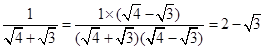（1）在计算结果中找出规律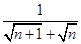=      （n表示大于0的自然数）
（2）通过上述化简过程，可知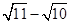      （填“＞”、“＜”或“=”）；
（3）利用你发现的规律计算下列式子的值：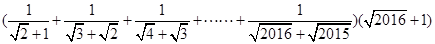

（1）计算：﹣×；
（2）先化简，再求值：（1﹣）÷，其中a=﹣．

阅读下列材料，然后回答问题：
在进行二次根式运算时，我们有时会碰上如、这样的式子，其实我们还可以将其进一步化简：； 。以上这种化简过程叫做分母有理化。   还可以用以下方法化简：
 
(1)请用其中一种方法化简
(2)化简：

（本小题6分）x、y为实数，且，求的值

先化简，再求值：（1+）•，其中x=+1．

数学张老师在课堂上提出一个问题：“通过探究知道：≈1．414…，它是个无限不循环小数，也叫无理数，它的整数部分是1，那么有谁能说出它的小数部分是多少”，小明举手回答：它的小数部分我们无法全部写出来，但可以用－1来表示它的小数部分，张老师夸奖小明真聪明，肯定了他的说法．现请你根据小明的说法解答：已知8+=x+y，其中x是一个整数，0＜y＜1，求3x+（y－）²⁰¹⁵的值．

y=，求3+2的算术平方根．

求代数式÷（﹣）的值，其中x=+1．

化简求值：，其中．