某地为更好治理湖水水质,治污部门决定购买10台污水处理设备.现有 两种型号的设备,其中每台的价格,月处理污水量如下表:
两种型号的设备,其中每台的价格,月处理污水量如下表:
| |
 型 型 |
 型 型 |
| 价格(万元/台) |
 |
 |
| 处理污水量(吨/月) |
240 |
200 |
经调查:购买一台 型设备比购买一台
型设备比购买一台 型设备多2万元,购买2台
型设备多2万元,购买2台 型设备比购买3台
型设备比购买3台 型设备少6万元.
型设备少6万元.
(1)求 的值.
的值.
(2)经预算:治污部门购买污水处理设备的资金不超过105万元,你认为该部门有哪几种购买方案.
(3)在(2)问的条件下,若每月要求处理的污水量不低于2040吨,为了节约资金,请你为治污部门设计一种最省钱的购买方案.
小武新家装修,在装修客厅时,购进彩色地砖和单色地砖共100块,共花费5600元.已知彩色地砖的单价是80元/块,单色地砖的单价是40元/块.
(1)两种型号的地砖各采购了多少块?
(2)如果厨房也要铺设这两种型号的地砖共60块,且采购地砖的费用不超过3200元,那么彩色地砖最多能采购多少块?
阅读下列材料:
解答“已知x﹣y=2,且x>1,y<0,试确定x+y的取值范围”有如下解法:
解:∵x﹣y=2,又∵x>1,∴y+2>1y>﹣1
又y<0,∴﹣1<y<0.…①
同理得:1<x<2.…②
由①+②得﹣1+1<y+x<0+2,∴x+y的取值范围是0<x+y<2.
请按照上述方法,完成下列问题:
已知关于x、y的方程组 的解都为正数.
的解都为正数.
(1)求a的取值范围;
(2)已知a﹣b=4,且a>1,求a+b的取值范围;
(3)已知a﹣b=m(m是大于0的常数),且b≤1,求2a+ b最大值.(用含m的代数式表示)
b最大值.(用含m的代数式表示)
某蔬菜培育中心决定向某灾区配送无辐射蔬菜和水果共3200箱,其中水果比蔬菜多800箱.
(1)求水果和蔬菜各有多少箱?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批水果和蔬菜全部运往该乡中小学.已知每辆甲种货车最多可装水果400箱和蔬菜100箱,每辆乙种货车最多可装水果和蔬菜各200箱,则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来;
(3)在(2)的条件下,如果甲种货车每辆需付运费4000元,乙种货车每辆需付运费
3600元.运输部门应选择哪种方案可使运费最少?最少运费是多少元?
已知关于x的方程4x+2m+1=2x+5的解是负数.
(1)求m的取值范围;
(2)在(1)的条件下,解关于x的不等式2(x﹣2)>mx+3.
定义符号 的含义为:当
的含义为:当 时,
时, 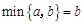 ;当
;当 时,
时,  .如:
.如: ,
, .
.
(1)求 ;
;
(2)已知 , 求实数
, 求实数 的取值范围;
的取值范围;
(3)当 时,
时, .直接写出实数
.直接写出实数 的取值范围.
的取值范围.
某校七年级共有200名学生,在一次数学测验后,为了解本次测验的成绩情况,从中随机抽取了部分学生的成绩进行统计,并制作了如下图表:

请你根据以上信息,解答下列问题:
(1)写出a,b,d的值并补全条形图;
(2)请你估计该校七年级共有多少名学生本次成绩不低于80分.
我县某汽车销售公司经销某品牌A款汽车,随着汽车的普及,其价格也在不断下降,今年5月份A款汽车的售价比去年同期每辆降价1万元,如果卖出相同数量的A款汽车,去年销售额为100万元,今年销售额只有90万元.
(1)今年5月份A款汽车每辆售价多少万元?
(2)为了增加收入,汽车销售公司决定再经销同品牌的B款汽车,已知A款汽车每辆进价7.5万元,B款汽车每辆进价为6万元,公司预计用不多于105万元且不少于99万元的资金购进这两款汽车共15辆,有几种进货方案?
(3)如果B款汽车每辆售价为8万元,为打开B款汽车的销路,公司决定每售出一辆B款汽车,返还顾客现金a万元,要使(2)中所有的方案获利相同,a值应是多少?此时,哪种方案对公司更有利?
两个数的大小关系可以通过它们的差来判断.若两个数a和b比较大小,则有:当a>b时,一定有a-b>0;当a=b时,一定有a-b=0;当a<b时,一定有a-b<0.反过来也成立,即:当a-b>0时,一定有a>b;当a-b=0时,一定有a=b;当a-b<0时,一定有a<b.因此,我们经常把两个要比较的对象先数量化,再求它们的差,根据差的正、负判断两个对象的大小关系.
根据上述结论,试比较x4+2x2+1与x4+x2+1的大小.
试题篮
()