初中数学含绝对值的一元一次不等式解答题

﹣（本题12分）在一平直河岸同侧有两个村庄，到的距离分别是3km和2km，．现计划在河岸上建一抽水站，用输水管向两个村庄供水．
方案设计
某班数学兴趣小组设计了两种铺设管道方案：图（1）是方案一的示意图，设该方案中管道长度为，且（其中于点）；图（2）是方案二的示意图，设该方案中管道长度为，且（其中点与点关于对称，与交于点）．

 
（1）观察计算
在方案一中，        km（用含的式子表示）；
在方案二中，组长小宇为了计算的长，作了如图（3）所示的辅助线，请你按小宇同学的思路计算，        km（用含的式子表示）．
（2）探索归纳
①当时，比较大小：（填“＞”、“＝”或“＜”）；
当时，比较大小：（填“＞”、“＝”或“＜”）；
②请你参考右边方框中的方法指导，
就（当时）的所有取值情况进
行分析，要使铺设的管道长度较短，
应选择方案一还是方案二？

（本小题满分7分）
解不等式组，并将它的解集在数轴上标出来．

解不等式组并写出不等式组的整数解．

学校计划选购甲、乙两种图书作为“校园读书节”的奖品．已知甲图书的单价是乙图书单价的1.5倍；用600元单独购买甲种图书比单独购买乙种图书要少10本．
（1）甲、乙两种图书的单价分别为多少元？
（2）若学校计划购买这两种图书共40本，且投入的经费不超过1050元，要使购买的甲种图书数量不少于乙种图书的数量，则共有几种购买方案？

（本题10分）若不等式组的解集是，
（1）求代数式的值；
（2）若，，为某三角形的三边长，试求的值．

上海某宾馆客房部有三人普通间和二人普通间，每间收费标准如下表所示．世博会期间，一个由50名女工组成的旅游团人住该宾馆，她们都选择了三人普通间和二人普通间，且每间正好都住满．设该旅游团人住三人普通间有x间．
(1)该旅游团人住的二人普通间有________间(用含x的代数式表示)；
(2)该旅游团要求一天的住宿费必须少于4500元，且入住的三人普通间不多于二人普通间．若客房部能满
足该旅游团的要求，那么该客房部有哪几种安排方案?

客房	普通间(元／天)
三人间	240
二人间	200

一次函数y=kx+b的图像经过点（0，-4）且与正比例函数y=k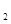x的图象交于点（2，-1）．
（1）分别求出这两个函数的表达式；
（2）求这两个函数的图象与x轴围成的三角形的面积；       
（3）直接写出不等式kx-4≥k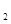x的解集。

某酒厂生产A，B两种品牌的酒，每天两种酒共生产700瓶，每种酒每瓶的成本
和利润如下表所示，设每天共获利y元，每天生产A种品牌的酒x瓶．
（1）请写出y关于x的关系式；
（2）如果该厂每天至少投入成本30000元，那么每天至少获利多少元？
（3）要使每天的利润率最大，应生产A，B两种酒各多少瓶？

	A	B
成本（元）	50	35
利润（元）	20	15

 

为支援四川雅安地震灾区，某市民政局组织募捐了240吨救灾物资，现准备租用甲、乙两种货车，将这批救灾物资一次性全部运往灾区，它们的载货量和租金如下表：

	甲种货车	乙种货车
载货量（吨/辆）	45	30
租金（元/辆）	400	300

如果计划租用6辆货车，且租车的总费用不超过2300元，求最省钱的租车方案.

生活中，在分析研究比赛成绩时经常要考虑不等关系．例如：一射击运动员在一次比赛中将进行10次射击，已知前7次射击共中61环，如果他要打破88环（每次射击以1到10的整数环计数）的记录，问第8次射击不能少于多少环？
我们可以按以下思路分析：
首先根据最后二次射击的总成绩可能出现的情况，来确定要打破88环的记录，第8次射击需要得到的成绩，并完成下表：

最后二次射击总成绩	第8次射击需得成绩
20环
19环
18环

根据以上分析可得如下解答：
解：设第8次射击的成绩为x环，则可列出一个关于x的不等式：（    ）解得（    ）
所以第8次设计不能少于 (     )环

某校志愿者团队在重阳节购买了一批牛奶到“夕阳红”敬老院
慰问孤寡老人，如果给每个老人分5盒，则剩下38盒，如果给每个老人分6盒，则最后一
个老人不足5盒，但至少分得一盒．
（1）设敬老院有名老人，则这批牛奶共有多少盒？（用含的代数式表示）．
（2）该敬老院至少有多少名老人？最多有多少名老人？

郑州市花卉种植专业户王有才承包了30亩花圃，分别种植康乃馨和玫瑰花，有关成本、销售额见下表：

种植种类	成本（万元/亩）	销售额（万元/亩）
康乃馨	2.4	3
玫瑰花	2	2.5

（1）2012年，王有才种植康乃馨20亩、玫瑰花10亩，求王有才这一年共收益多少万元？（收益=销售额-成本）
（2）2013年，王有才继续用这30亩花圃全部种植康乃馨和玫瑰花，计划投入成本不超过70万元.若每亩种植的成本、销售额与2012年相同，要获得最大收益，他应种植康乃馨和玫瑰花各多少亩？
（3）已知康乃馨每亩需要化肥500kg,玫瑰花每亩需要化肥700kg，根据（2）中的种植亩数，为了节约运输成本，实际使用的运输车辆每次装载化肥的总量是原计划每次装载总量的2倍，结果运输全部化肥比原计划减少2次.求王有才原定的运输车辆每次可装载化肥多少千克？

2013年4月20日，四川雅安发生7.0级地震，给雅安人民的生命财产带来巨大损失．某市民政部门将租用甲、乙两种货车共16辆，把粮食266吨、副食品169吨全部运到灾区．已知一辆甲种货车同时可装粮食18吨、副食品10吨；一辆乙种货车同时可装粮食16吨、副食11吨．
（1）若将这批货物一次性运到灾区，有哪几种租车方案？
（2）若甲种货车每辆需付燃油费1500元；乙种货车每辆需付燃油费1200元，应选（1）中的哪种方案，才能使所付的费用最少？最少费用是多少元？

小明参加学校组织的知识竞赛，共有道题．答对一题记分，答错（或不答）一题记分，小明参加本次竞赛要超过分，他至少要答对多少道题？

对x，y定义一种新运算T，规定：T（x，y）=（其中a、b均为非零常数），这里等式右边是通常的四则运算，例如：T（0，1）==b．
（1）已知T（1，-1）=-2，T（4，2）=1．
①求a，b的值；
②若关于m的不等式组恰好有3个整数解，求实数p的取值范围；
（2）若T（x，y）=T（y，x）对任意实数x，y都成立（这里T（x，y）和T（y，x）均有意义），则a，b应满足怎样的关系式？