初中数学一元二次方程的最值解答题

用适当的方法解方程．
（1）4x²-x-1=3x-2
（2）2y²+7y-3=0．

某超市销售一种旅游纪念品，平均每天可售出20套，每套盈利40元．“十一”期间，商场决定采取适当的降价措施，扩大销售量，增加盈利，尽快减少库存．经市场调查发现：如果每套降价1元，那么平均每天就可多售出2套．要想平均每天销售这种纪念品盈利1200元，那么每套应降价多少元？

阅读下列例题：
解方程x²-|x|-2=0
解：（1）当x≥0时，原方程化为x²-x-2=0，解得x₁=2，x₂=-1（舍去）．
当x＜0时，原方程化为x²+x-2=0，解得x₁=1（舍去），x₂=-2．
∴x₁=2，x₂=-2是原方程的根．
请参照例题解方程：x²-|x-1|-1=0．

小明在一幅长为80cm，宽为50cm的矩形风景画的四周镶一条相同宽度的金色纸边，制成一幅矩形挂图，如图所示，如果要使整个挂图的面积是5400cm²，求金色纸边的宽度．

解下列方程
（1）x（2x-7）=3x
（2）x²-2x-3=0．

2013年，江阴市某楼盘以每平方米6500元的均价对外销售，因为楼盘滞销，房地产开发商为了加快资金周转，决定进行降价促销，经过连续两年下调后，2015年的均价为每平方米5265元．
（1）求平均每年下调的百分率；
（2）假设2016年的均价仍然下调相同的百分率，张强准备购买一套100平方米的住房，他持有现金20万元，可以在银行贷款30万元，张强的愿望能否实现？（房价每平方米按照均价计算）

先化简，再计算：，其中是方程的正数根．

解下列方程
（1）     
（2）   
（3）（配方法）

某养殖户每年的养殖成本包括固定成本和可变成本，其中固定成本每年均为3万元，可变成本逐年增长，已知该养殖户第1年的可变成本为2．4万元，设可变成本平均每年增长的百分率为x．
（1）用含x的代数式表示第3年的可变成本为  万元．
（2）如果该养殖户第3年的养殖成本为6．456万元，求可变成本平均每年增长的百分率？

已知关于x的一元二次方程x²－6x＋k＝0有实数根．
（1）求k的取值范围；
（2）如果k取符合条件的最大整数，且一元二次方程x²－6x＋k＝0与x²＋mx－1＝0有一个相同的根，求常数m的值．

解方程
（1）（4x－1）²－9＝0
（2）x²―3x―2＝0

已知关于x的一元二次方程x²－2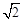x＋m＝0有两个不相等的实数根．
（1）求实数m的最大整数值；
（2）在（1）的条件下，方程的实数根是x₁，x₂（x₁>x₂），求代数式x₁＋2x₂的值．

已知关于x的方程x²－6x＋m²－3m＝0的一根为2．
（1）求5m²－15m－100的值； 
（2）求方程的另一根．

解方程：x²－6x－7＝0．

如图，平面直角坐标系中，直线l分别交x轴、y轴于A、B两点（OA＜OB），且OA、OB的长分别是一元二次方程x²-（＋1）x＋＝0的两个根．点C在x轴负半轴上，且AB：AC＝1：2．

（1）求A、C两点的坐标．
（2）若点M从点C出发，以每秒1个单位的速度沿射线CB运动，连接AM，设△ABM的面积为S，点M的运动时间为t，写出S关于t的函数关系式，并写出自变量的取值范围．
（3）点P是y轴上的点，在坐标平面内是否存在点Q，使以A、B、P、Q为顶点的四边形是菱形？若存在，请直接写出Q点的坐标；若不存在，说明理由．