初中数学一元二次方程的最值解答题

解方程：2x²-9x+8=0．

某软件商店经销一种热门益智游戏软件，进货成本为每盘8元，若按每盘10元销售，每天能售出200盘；但由于货源紧缺，商店决定采用尽量提高软件售价减少销售量的办法增加利润，如果这种软件每盘售价提高2元其销售量就减少40盘，问应将每盘售价定为多少元时，才能使每天利润为640元？这时的销售量应为多少？

（1）2x²-9x+8=0（用公式法）         
（2）3x²-4x-6=0（配方法解）
（3）（x-2）²=（2x+3）²（用合适的方法）  
（4）（5x-1）²-3（5x-1）=0（用合适的方法）

有一种传染性疾病，蔓延速度极快．据统汁，在人群密集的某城市里，通常情况下，每人一天能传染给若干人，通过计算解答下面的问题：
（1）现有一人患了这种疾病，开始两天共有225人患上此病，求每天一人传染了几人？
（2）两天后，人们有所觉察，这样平均一个人一天以少传播5人的速度在递减，求再过两天共有多少人患有此病？

解方程
（1）（x-1）²=4
（2）3x²+5（2x+1）=0
（3）x²-3x-4=0
（4）（y+2）²=（3y-1）²．

对x，y定义一种新运算T，规定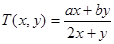：（其中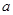、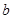均为非零常数），这里等式右边是通常的四则运算，例如：．
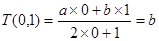（1）已知T（1，﹣1）=﹣2，T（4，2）=1．
①求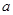、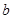的值；
②若关于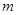的方程T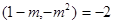有实数解，求实数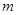的值；
（2）若T（x，y）=T（y，x）对任意实数x，y都成立（这里T（x，y）和T（y，x）均有意义），则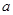、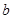应满足怎样的关系式？

为满足市场需求，某超市在中秋节来临前夕，购进一种品牌月饼，每盒进价是40元．超市规定每盒售价不得少于45元．根据以往销售经验发现；当售价定为每盒45元时，每天可以卖出1600盒，每盒售价每提高1元，每天要少卖出20盒．
（1）当每盒售价定为多少元时，每天销售的利润P（元）最大？最大利润是多少？
（2）为稳定物价，有关管理部门限定：这种粽子的每盒售价不得高于58元．如果超市想要每天获得6000元的利润，那么超市每天销售月饼多少盒？

我校初2016级举行了初三体育测试，现随机抽取了部分学生的成绩为样本，按 A(优秀)、B（良好）、C（及格）、D（不及格）四个等级进行统计，并将统计结果制成如下统计图．如图，请你结合图表所给信息解答下列问题：

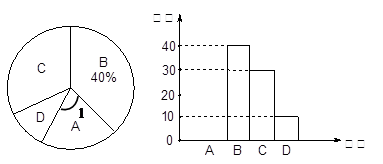
（1）本次调查共随机抽取了_______名学生，其中∠1=        
（2）将条形统计图在图中补充完整；
（3）初2016级目前举行了四次体育测试．小新同学第一次成绩为25分，第三次测试成绩为36分，若每次体育期末考试小欣体育成绩的增长率相同，求出这个增长率．

解一元二次方程．

某汽车销售公司2013年盈利1500万元，到2015年盈利2160万元，且从2013年到2015年，每年盈利的年增长率相同．
（1）该公司2013年至2015年盈利的年增长率?
（2）若该公司盈利的年增长率继续保持不变，预计2016年盈利多少万元?

已知x₁，x₂是一元二次方程的两个实数根．
（1）求实数m的取值范围；
（2）如果x₁，x₂满足不等式，且m为整数，求m的值．

先化简，再求值：，其中是2x²-2x-7=0的根．

解方程：
（1） （用配方法解）
（2）3x（x－1）=2－2x（用适当的方法解）

请同学们认真阅读下面的一段文字材料，然后解答题目中提出的有关问题．
为解方程，我们可以将视为一个整体，然后设，则原方程可化为 ①
解得，，当y=1时，，∴，；
当y=4时，，∴，，∴原方程的解为=， =－，=，=－．
解答问题：
（1）填空：在由原方程得到方程①的过程中，利用_________法达到了降次的目的，体现了_________的数学思想．
（2）解方程．

解方程：
（1）；                      
（2）