阅读材料:用配方法求最值.已知x,y为非负实数,
∵x+y﹣2 ≥0
≥0
∴x+y≥2 ,当且仅当“x=y”时,等号成立.
,当且仅当“x=y”时,等号成立.
示例:当x>0时,求y=x+ +4的最小值.
+4的最小值.
解: +4=6,当x=
+4=6,当x= ,即x=1时,y的最小值为6.
,即x=1时,y的最小值为6.
(1)尝试:当x>0时,求y= 的最小值.
的最小值.
(2)问题解决:随着人们生活水平的快速提高,小轿车已成为越来越多家庭的交通工具,假设某种小轿车的购车费用为10万元,每年应缴保险费等各类费用共计0.4万元,n年的保养、维护费用总和为 万元.问这种小轿车使用多少年报废最合算(即:使用多少年的年平均费用最少,年平均费用=
万元.问这种小轿车使用多少年报废最合算(即:使用多少年的年平均费用最少,年平均费用= )?最少年平均费用为多少万元?
)?最少年平均费用为多少万元?
2013年,无锡市蠡湖新城某楼盘以每平方米12000元的均价对外销售.由于楼盘滞销,房地产商为了加快资金周转,决定进行降价促销,经过连续两年下调后,2015年该楼盘的均价为每平方米9720元.
(1)求平均每年下调的百分率;
(2)假设2016年该楼盘的均价仍然下调相同的百分率,李强准备购买一套100平方米的住房,他持有现金30万元,可在银行贷款50万元,李强的愿望能否实现?(房价按照均价计算,不考虑其它因素.)
已知关于x的一元二次方程x2-(m+6)x+3m+9=0的两个实数根分别为x1,x2.
(1)求证:该一元二次方程总有两个实数根;
(2)若n=4(x1+x2)-x1x2,判断动点P(m,n)所形成的函数图象是否经过点 A(1,16),并说明理由.
解方程
(1)(x-2)2=9;
(2)3x2-1=2 x(配方法);
(3)x2+3 x+1=0;
(4)(x+1)2-6(x+1)+5=0.
某种产品的年产量不超过1000t,该产品的年产量(t)与费用(万元)之间的函数关系如图(1);该产品的年销售量(t)与每吨销售价(万元)之间的函数关系如图(2).
(1)设产品的费用为y(万元),试写出y与t的函数关系式.
(2)若生产出的产品都能在当年销售完,则年产量为多少吨时,当年可获得7500万元毛利润?(毛利润=销售额-费用)
我们知道:对于任何实数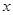 ,①∵
,①∵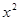 ≥0,∴
≥0,∴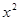 +1>0;
+1>0;
②∵ ≥0,∴
≥0,∴ +
+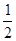 >0.
>0.
模仿上述方法解答:
求证:(1)对于任何实数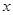 ,均有:2x2+4x+3>0;
,均有:2x2+4x+3>0;
(2)不论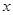 为何实数,多项式3x2-5x-1的值总大于2x2-4x-2的值.
为何实数,多项式3x2-5x-1的值总大于2x2-4x-2的值.
已知关于x的方程x2-2(k-3)x+k2-4k-1=0.
(1)若这个方程有实数根,求k的取值范围;
(2)若这个方程有一个根为1,求k的值;
阅读材料:为解方程(x2-1)2-5(x2-1)+4=0,我们可以将x2-1视为一个整体,然后设x2-1=y,则(x2-1)2=y2,原方程化为y2-5y+4=0.①
解得y1=1,y2=4
当y=1时,x2-1=1.∴x2=2.∴x=±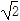 ;
;
当y=4时,x2-1=4,∴x2=5,∴x=±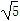 .
.
∴原方程的解为x1=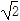 ,x2=-
,x2=-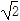 ,x3=
,x3=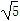 ,x4=-
,x4=-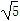 .
.
解方程:(x2+1)2-(x2+1)-6=0.
解方程.
(1)2x(x+3)=6(x+3)
(2)(2x-1)2=5
(3)y2-y=12
(4)2x2-5x+1=0
试题篮
()