如图,已知抛物线 经过A(2,0)、B(0,-6)两点,其对称轴与
经过A(2,0)、B(0,-6)两点,其对称轴与 轴交于点C.
轴交于点C.
(1)求该抛物线和直线BC的解析式;
(2)设抛物线与直线BC相交于点D,连结AB、AD,求△ABD的面积.
(满分14分)如图,抛物线经过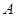 (
(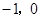 ),
), (
( ),
),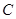 (
(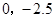 )三点.
)三点.
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点 ,使
,使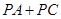 的值最小,求点
的值最小,求点 的坐标;
的坐标;
(3)点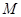 为
为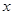 轴上一动点,在抛物线上是否存在点
轴上一动点,在抛物线上是否存在点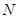 ,使得以
,使得以 四点为顶点的四边形为平行四边形?若存在,请直接写出点
四点为顶点的四边形为平行四边形?若存在,请直接写出点 的坐标.
的坐标.
已知抛物线 经过
经过 ,
, ,
, 。
。
(1)求此抛物线的解析式;
(2)求出顶点 的坐标,连接
的坐标,连接 ,求证△
,求证△ ∽△
∽△ ;
;
(3)在直线 上方的抛物线上是否存在一点M,使S△
上方的抛物线上是否存在一点M,使S△ 最大,求出M的坐标;
最大,求出M的坐标;
如图,在平面直角坐标系xOy中,正方形OABC的边长为2cm,点A、C别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B,最低点为M,且S△AMB= .
.
(1)求此抛物线的解析式,并说明这条抛物线是由抛物线y=ax2怎样平移得到的;
(2)如果点P由点A开始沿着射线AB以2cm/s的速度移动,同时点Q由点B开始沿BC边以1cm/s的速度向点C移动,当其中一点到达终点时运动结束;
①在运动过程中,P、Q两点间的距离是否存在最小值,如果存在,请求出它的最小值;
②当PQ取得最小值时,在抛物线上是否存在点R,使得以P、B、Q、R为顶点的四边形是梯形? 如果存在,求出R点的坐标,如果不存在,请说明理由.
已知:抛物线 .
.
(1)求证:不论a取何值时,抛物线 与x轴都有两个不同的交点.
与x轴都有两个不同的交点.
(2)设这个二次函数的图象与 轴相交于A(
轴相交于A( ,0),B(
,0),B( ,0),且
,0),且 、
、 的平方和为3,求a的值.
的平方和为3,求a的值.
抛物线y=﹣x2+(m﹣1)x+m与y轴交于点(0,3).
(1)求抛物线的解析式;
(2)求抛物线与坐标轴的交点坐标;
(3)①当x取什么值时,y>0?②当x取什么值时,y的值随x的增大而减小?
已知二次函数y=ax2+bx-3的图象经过点A(2,-3),B(-1,0).求二次函数的解析式
如图,抛物线经过A(4,0)、B(1,0)、C(0,-2)三点.
(1)求出抛物线的解析式;
(2)在直线AC上方的抛物线上有一动点D,当△ACD的面积最大时,求出点D的坐标;
(3)P是抛物线上一动点,过P作PM⊥x轴,垂足为M,是否存在P点,使得以A,P,M为顶点的三角形与△OAC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
已知抛物线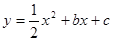 的图像经过点O(0,0)A(6,0)。
的图像经过点O(0,0)A(6,0)。
(1)b = ,c = ;
(2)点B是x正半轴上的一动点,以OB为边在第一象限作一个正方形OBCD,使其一个顶点在抛物线上(不包括B点 ),画出示意图,求点B的坐标;
(3)在(2)的条件下,点E是线段BC上的一个动点,连结DE交线段AC与点F,则线段DF是否存在最小值,如果存在,请求出结果,如果不存在,请说明理由;
在直角梯形ABCD中,∠D=90°,高CD= cm(如图1),动点P、Q同时从点A出发,点P沿AB、BC运动到点C停止,速度为1cm/s,点Q沿AD运动到点D停止,速度为2cm/s,而点P到达点B时,点Q正好到达点D,设P、Q同时从A点出发的时间为t(s)时,△APQ的面积为y(cm2)所形成的函数图象如图(2)所示,其中MN表示一条平行于X轴的线段.
cm(如图1),动点P、Q同时从点A出发,点P沿AB、BC运动到点C停止,速度为1cm/s,点Q沿AD运动到点D停止,速度为2cm/s,而点P到达点B时,点Q正好到达点D,设P、Q同时从A点出发的时间为t(s)时,△APQ的面积为y(cm2)所形成的函数图象如图(2)所示,其中MN表示一条平行于X轴的线段.
(1)求出BC的长和点M的坐标.
(2)当点P在线段AB上运动时,直线PQ截梯形所得三角形部分沿PQ向上折叠,设折叠后与梯形重叠部分的面积为S cm2,请求出S与t的函数关系式.
(3)在P、Q的整个运动过程中,将直线PQ截梯形所得三角形部分沿PQ折叠.是否存在某一时刻,使得折叠后与梯形重叠部分的面积为直角梯形ABCD面积的 ?若存在,求出t的值;若不存在,试说明理由.
?若存在,求出t的值;若不存在,试说明理由.
如图,抛物线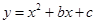 与
与 轴交于A(﹣2,0),B(6,0)两点.
轴交于A(﹣2,0),B(6,0)两点.
(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标;
(3)点P为y轴右侧抛物线上一个动点,若S△PAB=32,
求出此时P点的坐标.
试题篮
()