初中数学二次函数在给定区间上的最值解答题

已知：关于x的一元二次方程mx ²-（3m+2）x+2m+2=0（m>0）．
（1）求证：方程有两个不相等的实数根；
（2）设方程的两个实数根分别为x ₁，x ₂（其中x ₁< x ₂）．若y是关于x的函数，且y=x ₂-2x ₁，求这个函数的解析式．

已知一个二次函数y=ax ²+bx+c的图象如图所示，请求出这个二次函数的解析式。

杂技团进行杂技表演，演员从跷跷板右端A处弹跳到人梯顶端椅子B处，其身体（看成一点）的路线是抛物线y＝－3/5X²＋3X＋1的一部分，如图．

（1）求演员弹跳离地面的最大高度；
（2）已知人梯高BC＝3．4米，在一次表演中，人梯到起跳点A的水平距离是4米，问这次表演是否成功？请说明理由．

直线y=x+m和抛物线y=x²+bx+c都经过点A（1，0），B（3，2）．

（1）求m的值和抛物线的解析式；
（2）求不等式x²+bx+c＞x+m的解集．（直接写出答案）

如图所示，二次函数y=ax²+bx+c（a≠0）的图象与x轴交于A、B两点，与y轴交于C（0，2），若∠ACB=90°，BC=．

试求：（1）A、B两点的坐标；
（2）二次函数的表达式．

已知二次函数．
（1）求该函数图象的顶点坐标．
（2）求此抛物线与轴的交点坐标．

如图，二次函数y=﹣x²+bx+c的图象经过坐标原点，且与x轴交于A（﹣2，0）．

（1）求此二次函数解析式及顶点B的坐标；
（2）在抛物线上有一点P，满足S_△AOP=3，直接写出点P的坐标．

如图，二次函数y＝－x₂＋nx＋n²－9（n为常数）的图像经过坐标原点和x轴上另一点A，顶点在第一象限．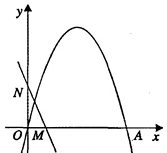

（1）求n的值和点A坐标；
（2）已知一次函数y＝－2x＋b（b >0）分别交x轴、y轴于M、N两点．点P是二次函数图像的y轴右侧部分上的一个动点，若PN⊥NM于N点，且△PMN与△OMN相似，求点P坐标．

已知二次函数y＝ax²＋bx＋1的图像经过（1，2），（2，4）两点．
（1）求a、b值；（2）试判断该函数图像与x轴的交点情况，并说明理由．

如图：△ABC是边长为4的等边三角形，AB在X轴上，点C在第一象限，AC与Y轴交于点D，点A的坐标为（-1，0）

（1）求 B、C、D三点的坐标；
（2）抛物线经过B、C、D三点，求它的解析式；

将Rt△ABC和Rt△DEF按图1摆放（点F与点A重合），点A、E、F、B在同一直线上，∠ACB＝∠DEF＝90°，∠BAC＝∠D＝30°，BC＝8cm，EF＝6cm．
如图2，△DEF从图1位置出发，以1cm/s的速度沿射线AB下滑，DE与AC相交于点H，DF与AC相交于点G，设下滑时间为t（s）（0＜t≤6）．
（1）当t为何值时，点G在线段AE的垂直平分线上？
（2）是否存在某一时刻t，使B、C、D三点在同一条直线上，若存在，求出t的值；若不存在，请说明理由；
（3）设△DEF与△ABC的重合部分的面积为S，直接写出S与t之间的函数关系式以及S的最大值（不需要给出解答过程）．

已知二次函数
（1）该函数图像的对称轴是        ，顶点坐标           ；
（2）选取适当的数据填入下表，并描点画出函数图像；

x	…						…
y	…						…

（3）求抛物线与坐标轴的交点坐标；
（4）利用图象直接回答当x为何值时，函数值y大于0？

如图，抛物线交x轴于A，B两点（A在B左侧），交y轴于点C．已知一次函数y=kx+b的图象过点A，C．

（1）求抛物线的对称轴和一次函数的解析式；
（2）根据图象，写出满足kx+b＞的x的取值范围；
（3）在平面直角坐标系xoy 中是否存在点P，与A、B、C三点构成一个平行四边形？若存在，请写出点P的坐标；若不存在，请说明理由．

随着农业科技的不断发展，农田灌溉也开始采用喷灌的形式（如图甲）．在田间安装一个离开地面一定高度且垂直于地面的喷头，喷头可旋转360．，喷出的水流呈抛物线形状．
如图乙，用OA表示垂直于地面MN的喷头，米，水流在与OA的距离10米时达到最高点，这时最高点离地面5米．如果不计其它因素，当喷头环绕一周后，能喷灌的最大直径是多少米（结果精确到0．1，参考数据）？

某商场将进价为1800元的电冰箱以每台2400元售出，平均每天能售出8台，为了配合国家“家电下乡”政策的实施，商场决定采取适当的降价措施．调查表明：这种冰箱的售价每降价50元，平均每天就能多售出4台．
（1）设每台冰箱降价元，商场每天销售这种冰箱的利润为元，求与之间的函数关系式（不要求写自变量的取值范围）．
（2）商场想在这种冰箱的销售中每天盈利8000元，同时又要使顾客得到实惠，每台冰箱应降价多少元？
（3）每台冰箱降价多少元时，商场每天销售这种冰箱的利润最高？最高利润是多少元？