初中数学二次函数在给定区间上的最值解答题

已知抛物线y=-mx²+4x+2m与x轴交于点A（α，0）， B（β，0），且．

（1）求抛物线的解析式．
（2）抛物线的对称轴为l，与y轴的交点为C，顶点为D，点C关于l的对称点为E．是否存在x轴上的点M、y轴上的点N，使四边形DNME的周长最小？若存在，请画出图形（保留作图痕迹），并求出周长的最小值；若不存在，请说明理由．
（3）若点P在抛物线上，点Q在x轴上，当以点D、E、P、Q为顶点的四边形是平行四边形时，求点P的坐标．

如图，已知一条直线过点，且与抛物线交于A，B两点，其中点A的横坐标是．
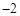（1）求这条直线的函数关系式及点B的坐标；
（2）在x轴上是否存在点C，使得△ABC是直角三角形？若存在，求出点C的坐标；若不存在，请说明理由；
（3） 过线段AB上一点P，作PM //x轴，交抛物线于点M，点M在第一象限，点N，当点M的横坐标为何值时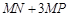，的长度最大？最大值是多少？

如图，在平面直角坐标系中，点M的坐标是（5，4），⊙M与y轴相切于点C，与x轴相交于A、B两点．

（1）则点A、B、C的坐标分别是A（__，__），B（__，__），C（__，__）；
（2）设经过A、B两点的抛物线解析式为，它的顶点为F，求证：直线FA与⊙M相切；
（3）在抛物线的对称轴上，是否存在点P，且点P在x轴的上方，使△PBC是等腰三角形．如果存在，请求出点P的坐标；如果不存在，请说明理由．

一块材料的形状是锐角三角形ABC，边BC=120mm，高AD=80mm，把它加工成正方形零件如图1，使正方形的一边在BC上，其余两个顶点分别在AB、AC上．

（1）求证：△AEF∽△ABC；
（2）求这个正方形零件的边长；
（3）如果把它加工成矩形零件如图2，问这个矩形的最大面积是多少？

（本题14分）如图，在平面直角坐标系内，正方形AOBC顶点C的坐标为（2，2），过点B的直线∥OC，P是直线上一个动点，抛物线过O、C、P三点．

（1）填空：直线的函数解析式为     ；的关系式是    ．
（2）当△PBC是等腰Rt△时，求抛物线的解析式 ；
（3）当抛物线的对称轴与正方形有交点时，直接写出点P横坐标的取值范围    ．

（本题12分）学校计划选购甲、乙两种图书作为“校园读书节”的奖品．已知甲图书的单价是乙图书单价的1．5倍；用600元单独购买甲种图书比单独购买乙种图书要少10本．
（1）甲、乙两种图书的单价分别为多少元？
（2）若学校计划购买这两种图书共40本，其中甲种图书a本，投入的经费为W元，
①请写出W关于a的函数关系式;
②若投入的经费不超过1050元，且使购买的甲种图书数量不少于乙种图书的数量，则共有几种购买方案? 并求出最节省的购买方案和最节省经费；
（3）若学校计划购买这两种图书总数超过30本,其中甲种图书a本，乙种图书b本,
且投入的经费恰好为690元，则b=   （ 写出两种可能的值）．

已知抛物线L₁：和抛物线L₂：，其中，抛物线L₂与x轴相交于A、B两点，其图像如图所示．
（1）下列说法你认为正确的序号是                   ；
①抛物线L₁和L₂与轴交于同一点F；  ② 抛物线L₁和L₂开口都向上；
③抛物线L₁和L₂的对称轴是同一条直线；      ④ A （-5，0）， B（-1，0）
（2）抛物线L₁和L₂相交于点E、F，当的值发生变化时，请判断线段EF的长度是否发生变化，并说明理由；
（3）在（2）中，若抛物线L₁的顶点为M，抛物线L₂的顶点为N. 问是否存在实数，使MN＝2EF，如存在，求出实数，如不存在，请说明理由.

在平面直角坐标系中，抛物线经过坐标原点O、点A（2，2）和点B（4，0）三个点，连接OA、OB．得到△OAB，点E在OA边上从点O向点A匀速运动（其中点E不与点A、O重合），同时点F以相同的速度在AB边上从点A向点B运动．
（1）求出该抛物线的解析式．
（2）若点C是线段OB的中点，连接CE、EF、FC，如图所示；

①在点E运动的过程中，四边形AECF的面积是否会随着点E位置的改变而发生变化?如果变化请说明理由；如果不变，请求出四边形AECF的面积；
②在点E运动的过程中，点A到线段EF的距离是否存在最大值，如果存在请求出最大距离；如果不存在，请说明理由．

如图，已知等边三角形ABC的边长为2，E、F、G分别是边AB、BC、CA的点，且AE=BF=CG，设△EFG的面积为，AE的长为，则与的函数图象大致是（   ）

（本小题满分14分）根据下列要求，解答相关问题.
（1）请补全以下求不等式的解集的过程.
①构造函数，画出图象：根据不等式特征构造二次函数；并在下面的坐标系中(见图1)画出二次函数的图象（只画出图象即可）.
②求得界点，标示所需：当y=0时，求得方程的解为                 ；并用锯齿线标示出函数图象中y≥0的部分.
③借助图象，写出解集：由所标示图象，可得不等式的解集为                     .
（2）利用（1）中求不等式解集的步骤，求不等式的解集.
①构造函数，画出图象：
②求得界点，标示所需：
③借助图像，写出解集：
（3）参照以上两个求不等式解集的过程，借助一元二次方程的求根公式，直接写出关于x的不等式
的解集.
          

（本小题满分10分）一种进价为每件40元的T恤，若销售单价为60元，则每周可卖出300件.为提高利润，欲对该T恤进行涨价销售.经过调查发现：每涨价1元，每周要少卖出10件.请确定该T恤涨价后每周的销售利润y（元）与销售单价x（元）之间的函数关系式，并求销售单价定为多少元时，每周的销售利润最大？

如图，已知二次函数：（）和二次函数：（）图象的顶点分别为M，N，与y轴分别交于点E，F．

（1）函数（）的最小值为     ，当二次函数，的y值同时随着x的增大而减小时，x的取值范围是               ；
（2）当EF=MN时，求a的值，并判断四边形ENFM的形状（直接写出，不必证明）；
（3）若二次函数的图象与x轴的右交点为A（m，0），当△AMN为等腰三角形时，求方程的解．

如图，已知二次函数L₁：y＝ax²－2ax＋a＋3（a＞0）和二次函数L₂：y＝－a（x＋1）²＋1（a＞0）图像的顶点分别为M，N，与y轴分别交于点E，F．

（1）函数y=ax²－2ax＋a＋3（a＞0）的最小值为       ；当二次函数L₁，L₂的y值同时随着x的增大而减小时，x的取值范围是        ；
（2）当EF=MN时，求a的值，并判断四边形ENFM的形状（直接写出，不必证明）；
（3）若二次函数L₂的图象与x轴的右交点为A（m，0），当△AMN为等腰三角形时，求方程－a（x＋1）²＋1＝0的解．

已知二次函数的图像经过点，对称轴是经过且平行于轴的直线。
（1）求、的值
（2）如图，一次函数的图像经过点，与轴相交于点，与二次函数的图像相交于另一点B，点B在点P的右侧，， 求一次函数的表达式。

已知关于x的一元二次方程：
（1）试判断原方程根的情况；
（2）若抛物线与轴交于两点，则，两点间的距离是否存在最大或最小值？若存在，求出这个值；若不存在，请说明理由．（友情提示：）