初中数学二次函数在给定区间上的最值解答题

有这样一个问题：探究函数的图象与性质.
小东根据学习函数的经验，对函数的图象与性质进行了探究.
下面是小东的探究过程，请补充完整：
（1）函数的自变量x的取值范围是____；
（2）下表是y与x的几组对应值.

求m的值：
（3）如下图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点.根据描出的点，画出该函数的图象：

（4）进一步探究发现，该函数图象在第一象限内的最低点的坐标是，结合函数的图象，写出该函数的其它性质（一条即可）：_________.

已知：抛物线y=x²+bx+c经过点（2，-3）和（4，5）．

（1）求抛物线的表达式及顶点坐标；
（2）将抛物线沿x轴翻折，得到图像G，求图像G的表达式；
（3）在（2）的条件下，当-2<x<2时，直线y=m与该图像有一个公共点，求m的值或取值范围．

在平面直角坐标系xOy中，抛物线与轴交于点A（0,3），与轴交于点B，C（点B在点C左侧）．

（1）求该抛物线的表达式及点B，C的坐标；
（2）抛物线的对称轴与轴交于点D，若直线经过点D和点E，求直线DE的表达式；
（3）在（2）的条件下，已知点P（，0），过点P作垂直于轴的直线交抛物线于点M，交直线DE于点N，若点M和点N中至少有一个点在轴下方，直接写出的取值范围．

如图1，若抛物线L₁的顶点A在抛物线L₂上，抛物线L₂的顶点B也在抛物线L₁上（点A与点B不重合），我们把这样的两抛物线L₁、L₂互称为“友好”抛物线．

（1）一条抛物线的“友好”抛物线有_______条．

A．1

B．2

C．3

D．无数

（2）如图2，已知抛物线L₃：与y轴交于点C，点C关于该抛物线对称轴的对称点为D，请求出以点D为顶点的L₃的“友好”抛物线L₄的表达式；
（3）若抛物线的“友好”抛物线的解析式为,请直接写出与的关系式为                      ．

已知关于x的一元二次方程 （k≠0）．

（1）求证：无论k取何值，方程总有两个实数根；
（2）点在抛物线上，其中，且和k均为整数，求A，B两点的坐标及k的值；
（3）设（2）中所求抛物线与y轴交于点C，问该抛物线上是否存在点E，使得，若存在，求出E点坐标，若不存在，说明理由．

已知二次函数．
（1）二次函数的顶点在轴上，求的值；
（2）若二次函数与轴的两个交点A、B均为整数点（坐标为整数的点），当为整数时，求A、B两点的坐标．

（本题12分）已知抛物线y=＋c与x轴交于A（－1，0），B两点，交y轴于点C
       
（1）求抛物线的解析式
（2）点E（m，n）是第二象限内一点，过点E作EF⊥x轴交抛物线于点F，过点F作FG⊥y轴于点G，连接CE、CF，若∠CEF=∠CFG，求n的值并直接写出m的取值范围（利用图1完成你的探究）
（3）如图2，点P是线段OB上一动点（不包括点O、B），PM⊥x轴交抛物线于点M，∠OBQ＝∠OMP，BQ交直线PM于点Q，设点P的横坐标为t，求△PBQ的周长

如图，在平面直角坐标系中，平行四边形如图放置，将此平行四边形绕点O顺时针旋转90°得到平行四边形．抛物线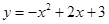经过点A、C、A′三点．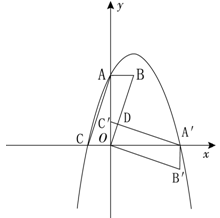

（1）求A、A′、C三点的坐标；
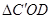（2）求平行四边形和平行四边形重叠部分的面积；
（3）点M是第一象限内抛物线上的一动点，问点M在何处时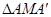，的面积最大？最大面积是多少？并写出此时M的坐标．

某公司新开发一种电子产品，现准备从国内和国外两种销售方案中选择一种进行销售．若只在国内销售，销售价格y（元/件）与月销量x（件）的函数关系式为y =x＋150，成本为20元/件，无论销售多少，每月还需支出广告费62500元，设月利润为w_内（元）（利润= 销售额－成本－广告费）．若只在国外销售，销售价格为150元/件，受各种不确定因素影响，成本为a元/件（a为常数，10≤a≤40），当月销量为x（件）时，每月还需缴纳x²元的附加费，设月利润为w_外（元）（利润=销售额－成本－附加费）．
（1）若在国内销售，当月销售量为1000件时，该产品的销售价格和月利润分别是多少元？当月销售量为多少件时，在国内销售的月利润最大？最大利润是多少？
（2）若在国外销售月利润的最大值与在国内销售月利润的最大值相同，求a的值；
（3）如果某月要将5000件产品全部销售完，请你通过分析帮公司决策，选择在国内还是在国外销售才能使所获月利润较大？

九（1）班数学兴趣小组经过市场调查，整理出某种商品在第x（1≤x≤90）天的售价与销量的相关信息如下表：

时间x（天）	1≤x＜50	50≤x≤90
售价（元/件）	x+40	90
每天销量（件）	200﹣2x

 
已知该商品的进价为每件30元，设销售该商品的每天利润为y元．
（1）求出y与x的函数关系式；
（2）问销售该商品第几天时，当天销售利润最大，最大利润是多少？
（3）该商品在销售过程中，共有多少天每天销售利润不低于4800元？请直接写出结果．

为了考察冰川融化的状况，一支科考队在某冰川上设定一个以大本营O为圆心，半径为4km 圆形考察区域，线段P₁P₂是冰川的部分边界线（不考虑其它边界），当冰川融化时，边界线沿着与其垂直的方向朝考察区域平行移动．若经过n年，冰川的边界线P₁P₂移动的距离为s（km），并且s与n（n为正整数）的关系是．以O为原点，建立如图所示的平面直角坐标系，其中P₁、P₂的坐标分别是（－4，9）、（－13，－3）．
 
（1）求线段P₁P₂所在的直线对应的函数关系式；
（2）求冰川的边界线移动到考察区域所需要的最短时间．

今年我市的蔬菜市场从5月份开始，由于本地蔬菜的上市，某种蔬菜的平均销售价格y（元/千克）从5月第1周的2．8元/千克下降至第2周的2．4元/千克，且y与周数x的变化情况满足二次函数：．
（1）求出5月份y与x所满足的二次函数关系式；
（2）若5月份的进价m（元/千克）与周数x所满足的函数关系为．求出5月份销售此种蔬菜一千克的利润W（元）与周数x的函数关系式，并求出在哪一周销售此种蔬菜一千克的利润最大？且最大利润是多少？

（本题12分） 如图，已知直线与轴交于点，与轴交于点，抛物线与直线交于、两点，与轴交于、两点，且点坐标为（1，0）．

（1）求该抛物线的解析式；
（2）动点在轴上移动，当△是直角三角形时，直接写出点的坐标；
（3）在抛物线的对称轴上找一点，使||的值最大，求出点的坐标．

如图，在平面直角坐标系中，抛物线经过点（1，﹣1），且对称轴为在线，点P、Q均在抛物线上，点P位于对称轴右侧，点Q位于对称轴左侧，PA垂直对称轴于点A，QB垂直对称轴于点B，且QB=PA+1，设点P的横坐标为．

（1）求这条抛物线所对应的函数关系式；
（2）求点Q的坐标（用含的式子表示）；
（3）请探究PA+QB=AB是否成立，并说明理由；
（4）抛物线（）经过Q、B、P三点，若其对称轴把四边形PAQB分成面积为1：5的两部分，直接写出此时的值．

如图，顶点为P（4，－4）的二次函数图象经过原点（0，0），点A在该图象上，OA交其对称轴于点M，点M、N关于点P对称，连接AN、ON

（1）求该二次函数的关系式．
（2）若点A的坐标是（6，－3），求△ANO的面积．