如图,已知抛物线y=ax2+bx+c(a≠0)经过A(﹣1,0),B(4,0),C(0,2)三点
(1)求这条抛物线的解析式;
(2)E为抛物线上一动点,是否存在点E使以A、B、E为顶点的三角形与△COB相似?若存在,试求出点E的坐标;若不存在,请说明理由;
如图,二次函数y=a +bx+c的图象交x轴于A、B两点,交y轴于点C.且B(1,0),若将△BOC绕点O逆时针旋转90°,所得△DOE的顶点E恰好与点A重合,且△ACD的面积为3.
+bx+c的图象交x轴于A、B两点,交y轴于点C.且B(1,0),若将△BOC绕点O逆时针旋转90°,所得△DOE的顶点E恰好与点A重合,且△ACD的面积为3.
(1)求这个二次函数的关系式.
(2)设这个二次函数图象的顶点为M,请在y轴上找一点P,使得△PAM的周长最小,并求出点P的坐标.
(3)设这个函数图象的对称轴l交x轴于点N,问:A、M、C、D、N这5个点是否会在同一个圆上?若在同一个圆上,请求出这个圆的圆心坐标,并作简要说明;若不可能,请说明理由.
在平面直角坐标系中,抛物线 与
与 轴交于A、B两点(点A在点B的左侧),与
轴交于A、B两点(点A在点B的左侧),与 轴交于点C,点B的坐标为(3,0),将直线
轴交于点C,点B的坐标为(3,0),将直线 沿
沿 轴向上平移3个单位长度后恰好经过B、C两点。
轴向上平移3个单位长度后恰好经过B、C两点。

(1)求直线BC及抛物线的解析式;
(2)设抛物线的顶点为D,点P在抛物线的对称轴上,且 ,求点P的坐标.
,求点P的坐标.
(3)连结CD,求∠OCA与∠OCD两角和的度数.
已知抛物线的表达式为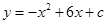

(1)若抛物线与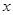 轴有交点,求
轴有交点,求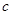 的取值范围;
的取值范围;
(2)设抛物线与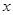 轴两个交点的横坐标分别为
轴两个交点的横坐标分别为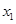 、
、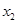 ,若
,若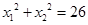 ,求
,求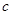 的值;
的值;
(3)若P、Q是抛物线上位于第一象限的不同两点,PA、QB都垂直于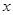 轴,垂足分别为A、B,且△OPA与△OQB全等,求证:
轴,垂足分别为A、B,且△OPA与△OQB全等,求证: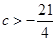
若关于x的二次函数y=a +bx+c(a>0,c>0,a、b、c是常数)与x轴交于两个不同的点A(
+bx+c(a>0,c>0,a、b、c是常数)与x轴交于两个不同的点A( ,0),B(
,0),B( ,0)(0<
,0)(0< <
< ),与y轴交于点P,其图像顶点为点M,点O为坐标原点。
),与y轴交于点P,其图像顶点为点M,点O为坐标原点。

(1)当 =c=2,a=
=c=2,a= 时,求
时,求 与b的值;
与b的值;
(2)当 =2c时,试问△ABM能否为等边三角形?判断并证明你的结论;
=2c时,试问△ABM能否为等边三角形?判断并证明你的结论;
(3)当 =mc(m>0)时,记△MAB,△PAB的面积分别为S1,S2,若△BPO∽△PAO,且S1=S2,求m的值。
=mc(m>0)时,记△MAB,△PAB的面积分别为S1,S2,若△BPO∽△PAO,且S1=S2,求m的值。
|
在直角坐标系中,我们不妨将横坐标,纵坐标均为整数的点称之为“中国结”。
(1)求函数y= x+2的图像上所有“中国结”的坐标;
x+2的图像上所有“中国结”的坐标;
(2)求函数y= (k≠0,k为常数)的图像上有且只有两个“中国结”,试求出常数k的值与相应“中国结”的坐标;
(k≠0,k为常数)的图像上有且只有两个“中国结”,试求出常数k的值与相应“中国结”的坐标;
(3)若二次函数y= (k为常数)的图像与x轴相交得到两个不同的“中国结”,试问该函数的图像与x轴所围成的平面图形中(含边界),一共包含有多少个“中国结”?
(k为常数)的图像与x轴相交得到两个不同的“中国结”,试问该函数的图像与x轴所围成的平面图形中(含边界),一共包含有多少个“中国结”?
(本题14分)如图,抛物线 与直线AB交于点A(-1,0),B(4,
与直线AB交于点A(-1,0),B(4, ).点D是抛物线A,B两点间部分上的一个动点(不与点A,B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.
).点D是抛物线A,B两点间部分上的一个动点(不与点A,B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.
(1)求抛物线的解析式;
(2)设点D的横坐标为m,△ADB的面积为S,求S关于m 的函数关系式,并求出当S 取最大值时的点C的坐标;
如图,在平面直角坐标系中,抛物线 与x轴交于点A(-2,0),B(4,0)两点,与x轴交于点C。
与x轴交于点A(-2,0),B(4,0)两点,与x轴交于点C。
(1)求抛物线的解析式;
(2)点P从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点Q从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动,当△PBQ存在时,求运动多少秒使△PBQ的面积最大,最大面积是多少?
(3)当△PBQ的面积最大时,在BC下方的抛物线上存在点K,使 ,求K点坐标。
,求K点坐标。
某产品每件成本10元 ,试销阶段每件产品的销售单价 (元 ∕ 件)与日销售量
(元 ∕ 件)与日销售量 (件)之间的关系如下表.
(件)之间的关系如下表.
 (元 ∕ 件) (元 ∕ 件) |
15 |
18 |
20 |
22 |
… |
 (件) (件) |
250 |
220 |
200 |
180 |
… |
(1)试判断 与
与 之间的函数关系,并求出函数关系式;
之间的函数关系,并求出函数关系式;
(2)求日销售利润w(元)与销售单价 (元 ∕ 件)之间的函数关系式;
(元 ∕ 件)之间的函数关系式;
(3)若规定销售单价不低于15元,且日销售量不少于120件,那么销售单价应定为多少时,每天获得的利润最大?最大利润是多少?
如图,抛物线y=-x2+(m+2)x-3(m-1)交x轴于A、B,交y轴于C.直线y=(m+1)x-3经过点A.
(1)求抛物线的解析式;
(2)点Q为线段AB上的动点,过点Q作QE∥AC,交BC于E,连CQ.当S△CQE的面积最大时,求点Q的坐标;
(3)直线y=kx(k<0)交直线y=(m+1)x-3于P,交抛物线y=-x2+(m+2)x-3(m-1)于点M,过M作x轴的垂线,垂足为D,交直线y=(m+1)x-3于N.△PMN能否为等腰三角形?若能,求k的值;若不能,说明理由.
红星公司生产的某种时令商品每件成本为20元,经过市场调研发现,这种商品在未来40天内的日销售量m(件)与时间t(天)的关系如下表:
时间 (天) (天) |
1 |
3 |
5 |
10 |
36 |
… |
| 日销售量m(件) |
94 |
90 |
86 |
76 |
24 |
… |
未来40天内,前20天每天的价格 (元/件)与时间
(元/件)与时间 (天)的函数关系式为
(天)的函数关系式为 (
( 且
且 为整数),后20天每天的价格
为整数),后20天每天的价格 (元/件)与时间
(元/件)与时间 (天)的函数关系式为
(天)的函数关系式为 (
( 且
且 为整数).
为整数).
(1)认真分析上表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据的m(件)与 (天)之间的关系式;
(天)之间的关系式;
(2)请预测未来40天中哪一天的日销售利润最大,最大日销售利润是多少?
(3)在实际销售的前20天中,该公司决定每销售一件商品就捐赠 元利润(
元利润( )给希望工程.公司通过销售记录发现,前20天中,每天扣除捐赠后的日销售利润随时间
)给希望工程.公司通过销售记录发现,前20天中,每天扣除捐赠后的日销售利润随时间 (天)的增大而增大,求
(天)的增大而增大,求 的取值范围.
的取值范围.
如图,已知直线y= x+1与y轴交于点A,与x轴交于点D,抛物线y=
x+1与y轴交于点A,与x轴交于点D,抛物线y= x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).
x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).
(1)求该抛物线的解析式;
(2)动点P在x轴上移动,当△PAE是直角三角形时,求点P的坐标P;
如图,已知抛物线 轴交于点A(-4,0)和B(1,0),与y轴交于C点.
轴交于点A(-4,0)和B(1,0),与y轴交于C点.
(1)求此抛物线的解析式;
(2)若P为抛物线上A、C两点间的一个动点,过P作y轴的平行线,交AC于Q,当P点运动到什么位置时,线段PQ的长最大,并求此时P点的坐标;
(3)设E是线段AB上的动点,作EF∥AC交BC于F,连接CE,当 的面积是
的面积是 面积的2倍时,求E点的坐标.
面积的2倍时,求E点的坐标.
如图,抛物线y=﹣(x﹣1)2+c与x轴交于A,B(A,B分别在y轴的左右两侧)两点,与y轴的正半轴交于点C,顶点为D,已知A(﹣1,0).
(1)求点B,C的坐标;
(2)将△COB沿x轴向右平移t个单位长度(0<t<3)得到△QPE.△QPE与△CDB重叠部分(如图中阴影部分)面积为S,求S与t的函数关系式,并写出自变量t的取值范围.
试题篮
()