(本题12分)如图,已知 ,
, 是一次函数
是一次函数 的图象和反比例函数
的图象和反比例函数 的图象的两个交点.
的图象的两个交点.
(1)求一次函数、反比例函数的关系式;
(2)求△AOB的面积.
(3)当自变量x满足什么条件时,y1>y2.(直接写出答案)(4)将反比例函数 的图象向右平移n(n>0)个单位,得到的新图象经过点(3,-4),求对应的函数关系式y3.(直接写出答案)
的图象向右平移n(n>0)个单位,得到的新图象经过点(3,-4),求对应的函数关系式y3.(直接写出答案)
一家图文广告公司制作的宣传画板颇受商家欢迎,这种画板的厚度忽略不计,形状均为正方形,边长在10~30dm之间.每张画板的成本价(单位:元)与它的面积(单位:dm2)成正比例,每张画板的出售价(单位:元)由基础价和浮动价两部分组成,其中基础价与画板的大小无关,是固定不变的.浮动价与画板的边长成正比例.在营销过程中得到了表格中的数据.
(1)求一张画板的出售价与边长之间满足的函数关系式
(2)已知出售一张边长为30dm的画板,获得的利润为130元(利润=出售价-成本价),
①求一张画板的利润与边长之间满足的函数关系式。
②当边长为多少时,出售一张画板所获得的利润最大?最大利润是多少?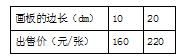
已知抛物线与x轴交于A(-3,0)、B(1,0)两点,交y轴于点C(0,-3),点E为直线AC上的一动点,DE∥y轴交抛物线于点D。
(1)求抛物线的解析式;
(2)当点E的坐标(-2,-1),连接AD,点P在x轴上,使∆APC与∆ADC全等,求出点P的坐标;
(3)当点E在直线AC上运动时,是否存在以D、E、O、C为顶点,OC为一边的平行四边形?若存在,试求出动点E的坐标;若不存在,请说明理由
某商场计划购进冰箱、彩电进行销售,相关信息如下表:
(1)若商场用80 000元购进冰箱的数量与用64 000元购进彩电的数量相等,求表中a的值.
(2)在(1)的条件下,为了满足市场需求,商场决定用不超过9万元采购冰箱、彩电共50台,且冰箱的数量不少于彩电数量的 .
.
①该商场有哪几种进货方式?
②若该商场将购进的冰箱、彩电全部售出,获得的最大利润为w元,请用所学的函数知识求出w的值.
如图,已知直线y=- x+2与坐标轴交于A、B两点,抛物线y=-
x+2与坐标轴交于A、B两点,抛物线y=- +bx+c与x轴交于A、C两点,与y轴交于点B.
+bx+c与x轴交于A、C两点,与y轴交于点B.
(1)求b、c的值.
(2)平行于y轴的直线x=2交直线AB于点D,交抛物线于点E.①点P从原点O出发,沿x轴正方向以1个单位/秒的速度运动,设运动时间为t,过点P作x轴的垂线与直线AB交于点F,与抛物线交于点G,当t为何值时,FG∶DE=1∶2?②将抛物线向上平移m(m>0)个单位后与y轴相交于点B′,与直线x=2相交于点E′,当E′O平分∠B′E′D时,求m的值.
(本题12分)东方专卖店专销某种品牌的计算器,进价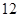 元/只,售价
元/只,售价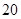 元/只.为了促销,专卖店决定凡是买
元/只.为了促销,专卖店决定凡是买 只以上的,每多买一只,售价就降低
只以上的,每多买一只,售价就降低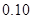 元(例如,某人买
元(例如,某人买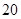 只计算器,于是每只降价
只计算器,于是每只降价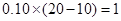 元,就可以按
元,就可以按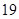 元/只的价格购买),但是最低价为
元/只的价格购买),但是最低价为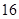 元/只.
元/只.
(1)求顾客一次至少买多少只,才能以最低价购买?
(2)写出当一次购买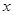 只时(
只时(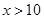 ),利润
),利润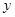 (元)与购买量
(元)与购买量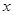 (只)之间的函数关系式;
(只)之间的函数关系式;
(3)有一天,一位顾客买了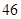 只,另一位顾客买了
只,另一位顾客买了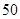 只,专卖店发现卖了
只,专卖店发现卖了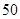 只反而比卖了
只反而比卖了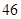 只赚的钱少,为了使每次卖得多赚钱也多,在其他促销条件不变的情况下,最低价
只赚的钱少,为了使每次卖得多赚钱也多,在其他促销条件不变的情况下,最低价 元/只至少要提高到多少元?
元/只至少要提高到多少元?
如图,矩形OABC的两边在坐标轴上,连接AC,抛物线y=x2-4x-2经过A,B两点.
(1)求A点坐标及线段AB的长;
(2)若点P由点A出发以每秒1个单位的速度沿AB边向点B移动,1秒后点Q也由点A出发以每秒7个单位的速度沿A-O-C-B的方向向点B移动,当其中一个点到达终点时另一个点也停止移动,点P的移动时间为t秒.
①当PQ⊥AC时,求t的值;
②当PQ∥AC时,对于抛物线对称轴上一点H,当点H的纵坐标满足条件_________时,∠HOQ<∠POQ.(直接写出答案)
如图,在平面直角坐标系中,将一块等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(-1,0),点A的坐标为(0,2)点B在
抛物线y=ax 2+ax-2上.
(1)点B的坐标为_____________; 抛物线的关系式为________________________;
(2)若点D是(1)中所求抛物线在第三象限内的一个动点,连接BD、CD.当△BCD的面积最大时,求点D的坐标;
(3)若将三角板ABC沿射线BC平移得到△A ′B ′C′,当C ′ 在抛物线上时.问此时四边形AC C ′A ′是什么特殊四边形?请证明?并判断点A ′是否在抛物线上,请说明理由;
如图1,已知抛物线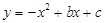 与一直线相交于
与一直线相交于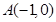 ,
,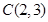 两点,与
两点,与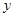 轴交于点
轴交于点 ,其顶点为
,其顶点为 .
.
(1)求抛物线及直线 的函数关系式,并直接写出点
的函数关系式,并直接写出点 的坐标;
的坐标;
(2)如图1,若抛物线的对称轴与直线 相交于点
相交于点 ,
, 为直线
为直线 上的任意一点,过点
上的任意一点,过点 作
作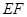 ∥
∥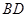 交抛物线于点
交抛物线于点 ,以
,以 ,
, ,
, ,
, 为顶点的四边形能否为平行四边形?若能,求点
为顶点的四边形能否为平行四边形?若能,求点 的坐标;若不能,请说明理由;
的坐标;若不能,请说明理由;
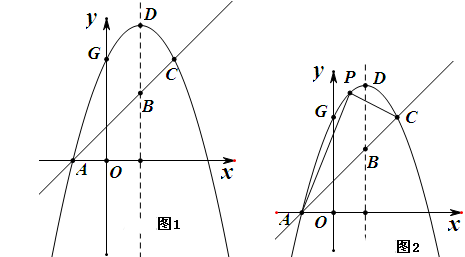
(3)如图2,若点 是抛物线上位于直线
是抛物线上位于直线 上方的一个动点,求
上方的一个动点,求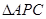 的面积的最大值.
的面积的最大值.
如图①,是某设计师设计的一建筑物造型的纵截面,曲线 是一开口向右、对称轴正好是水
是一开口向右、对称轴正好是水
平线 的抛物线的一部分,
的抛物线的一部分,  、
、 是与水平线
是与水平线 垂直的两根支柱,
垂直的两根支柱, =5米,
=5米, =3米,
=3米, =3米.
=3米.


(1)请你利用所学的函数知识求 的长(在所给的方框内画出函数图象的草图,并在图中标出点O、A、
的长(在所给的方框内画出函数图象的草图,并在图中标出点O、A、
B、C、D对应的位置);
(2)为了安全美观,准备拆除支柱 、
、 ,在水平线
,在水平线 上另找一点
上另找一点 作为地面上的支撑点,用固定材
作为地面上的支撑点,用固定材
料连接 、
、 ,对抛物线造型进行支撑加固.(如图②)
,对抛物线造型进行支撑加固.(如图②)
①为使用料最省,请在图②中作出用料最省时的点 的位置;(支柱与地面、造型连接处的用料多少问题
的位置;(支柱与地面、造型连接处的用料多少问题
暂不考虑)
②计算用料最省时点 、
、 之间的距离是多少?
之间的距离是多少?
某商店经营儿童益智玩具,已知成批购进时的单价是20元.调查发现:销售单价是30元时,月销售量是230件,而销售单价每上涨l元,月销售量就减少10件,但每件玩具售价不能高于40元.设每件玩具的销售单价上涨了x元时( 为正整数),月销售利润为y元.
(1)求y与x的函数关系式,并直接写出自变量x的取值范围.
(2)每件玩具的售价定为多少元时,月销售利润恰为2520元?
(3)每件玩具的售价定为多少元时,可使月销售利润最大?最大的月利润是多少?
(1)任选且只能选以下三个条件中的一个,求二次函数 的解析式;
的解析式;
① 随
随 变化的部分数值规律如下表:
变化的部分数值规律如下表:
②有序数对(-1,0),(1,4),(3,0)满足 ;
;
③已知函数 的图象的一部分(如图).
的图象的一部分(如图).
(2)直接写出二次函数 的三个性质.
的三个性质.
如图,抛物线 交x轴于A.B两点,A点坐标为(3,0),与y轴交于C(0,4),以OC.OA为边作矩形OADC交抛物线于点G.
交x轴于A.B两点,A点坐标为(3,0),与y轴交于C(0,4),以OC.OA为边作矩形OADC交抛物线于点G.
 (1)求抛物线的解析式;
(1)求抛物线的解析式;
(2)平行于抛物线对称轴的直线l在边OA(不包括O、A两点)上平行移动,分别交x轴于点E,交CD于点F,交AC于点M,交抛物线于点P,若点M的横坐标为m,请用含m的代数式表示PM的长,并求PM长的最大值。
(3)在(2)的条件下,连接PC,则在CD上方的抛物线部分是否存在这样的点P,使得以P、C.F为顶点的三角形和△AEM相似?若存在,求出此时m的值,并直接判断△PCM的形状;若不存在,请说明理由。
山地自行车越来越受到中学生的喜爱,各种品牌相继投放市场,某车行经营的A型车去年销售总额为5万元,今年每辆销售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少20%.
(1)今年A型车每辆售价多少元?(用列方程的方法解答)
(2)该车计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A,B两种型号车的进货和销售价格如下表:
| |
A型车 |
B型车 |
| 进货价格(元) |
1100 |
1400 |
| 销售价格(元) |
今年的销售价格 |
2000 |
试题篮
()