初中数学二次函数在给定区间上的最值解答题

在平面直角坐标系xOy中，抛物线与y轴交于C点，与x轴交于A，B两点（点A在点B左侧），且点A的横坐标为-1．

（1）求a的值；
（2）设抛物线的顶点P关于原点的对称点为，求点的坐标；
（3）将抛物线在A，B两点之间的部分（包括A， B两点），先向下平移3个单位，再向左平移m（）个单位，平移后的图象记为图象G，若图象G与直线无交点，求m的取值范围．

在平面直角坐标系xoy中，给出如下定义：形如y=a+a（x－m）与y=a－a（x－m）的两个二次函数的图象叫做“兄弟抛物线”．

（1）试写出一对兄弟抛物线的解析式                   与                   ；
（2）判断二次函数y=－x与y=－3x+2的图象是否为兄弟抛物线，如果是，求出a与m的值，如果不是，请说明理由；
（3）若一对兄弟抛物线各自与轴的两个交点和其顶点构成直角三角形，其中一个抛物线的对称轴为直线x=2且开口向上，请直接写出这对兄弟抛物线的解析式．

已知抛物线经过原点O及点A（-4，0）和点B（-6，3）．
        
（1）求抛物线的解析式以及顶点坐标；
（2）如图1，将直线沿y轴向下平移后与（1）中所求抛物线只有一个交点C，平移后的直线与y轴交于点D，求直线CD的解析式；
（3）如图2，将（1）中所求抛物线向上平移4个单位得到新抛物线，请直接写出新抛物线上到直线CD距离最短的点的坐标及该最短距离．

如图，在平面直角坐标系中，抛物线y=ax²+bx-3与x轴交于点A（-1，0）、B（3，0）两点，直线y=x-2与x轴交于点D．与y轴交于点C．点P是x轴下方的抛物[线上一动点，过点P作PF⊥x轴于点F，交直线CD于点E．设点P的横坐标为m．

（1）求抛物线的解析式：
（2）若PE=3EF，求m的值；
（3）连接PC，是否存在点P，使△PCE为等腰直角三角形？若存在，请直接写出相应的点P的横坐标m的值；若不存在，请说明理由．

如图1，关于的二次函数y=－+bx+c经过点A（－3,0），点C（0,3），点D为二次函数的顶点，DE为二次函数的对称轴，E在x轴上。

（1）求抛物线的解析式；
（2）DE上是否存在点P到AD的距离与到轴的距离相等，若存在求出点P，若不存在请说明理由；
（3）如图2，DE的左侧抛物线上是否存在点F，使2=3，若存在求出点F的坐标，若不存在请说明理由。

九年级数学兴趣小组经过市场调查，得到某种运动服每月的销量与售价的相关信息如下表：

售价（元/件）	100	110	120	130	…
月销量（件）	200	180	160	140	…

 
已知该运动服的进价为每件60元，设售价为元．
（1）请用含x的式子表示：①销售该运动服每件的利润是        元；②月销量是        件；（直接写出结果）
（2）设销售该运动服的月利润为元，那么售价为多少时，当月的利润最大，最大利润是多少？

已知二次函数
（1） 求证：不论k为何值，该函数的图像与x轴总有两个公共点；
（2） 该函数的图像与x轴交于A、B两点，与y轴交于点C。
当△ABC的面积等于2时，求k的值：
‚对任意负实数，当x＞m时，随着的增大而减小，试求出的一个值

利民商店经销甲、乙两种商品．现有如下信息:

请根据以上信息，解答下列问题：
（1）甲、乙两种商品的进货单价各多少元?
（2）该商店平均每天卖出甲商品500件和乙商品300件．经调查发现，甲、乙两种商品零售单价分别每降0．1元，这两种商品每天可各多销售100件．为了使每天获取更大的利润，商店决定把甲、乙两种商品的零售单价都下降m元．在不考虑其他因素的条件下，当m定为多少时，才能使商店每天销售甲、乙两种商品获取的利润最大？每天的最大利润是多少？

如图，已知抛物线y=ax²+bx+c（经过原点）与x轴相交于N点，直线y=kx+4与坐标轴分别相交于A、D两点，与抛物线相交于B（1，m）和C（2，2）两点．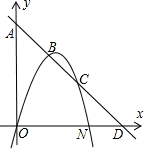

（1）求直线与抛物线的表达式；
（2）求证：C点是△AOD的外心；
（3）若（1）中的抛物线，在x轴上方的部分，有一动点P（x，y），设∠PON=α．当sinα为何值时，△PON的面积有最大值？
（4）若P点保持（3）中运动路线，是否存在△PON，使得其面积等于△OCN面积的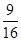？若存在，求出动点P的位置；若不存在，请说出理由．

如图，Rt△OAB中，∠OAB=90°，O为坐标原点，边OA在x轴上，OA=AB=1个单位长度．把Rt△OAB沿x轴正方向平移1个单位长度后得△AA₁B．

（1）求以A为顶点，且经过点B₁的抛物线的解析式；
（2）若（1）中的抛物线与OB交于点C，与y轴交于点D，求点D、C的坐标．

焚烧秸秆是造成雾霾的重要原因，某单位在科研部门的支持下，研发了一套设备，把秸秆转化为一种化工原料．已知该套设备每月的处理量最少为400吨，最多为600吨，月处理成本y（元）与月处理量x（吨）的函数关系为：y=x²-200x+80000，且每处理一吨秸秆得到的化工原料价值为100元．
（1）设每月获利为S元，求S（元）与x（吨）之间的函数关系式．
（2）该单位每月能否获利？如果获利，求出最大利润；如果不获利，则国家至少需要补贴多少元才能使该单位不亏损？

如图，C为∠AOB的边OA上一点，OC＝6，N为边OB上异于点O的一动点，P是线段CN上一点，过点P分别作PQ∥OA交OB于点Q，PM∥OB交OA于点M．

（1）若∠AOB＝60º，OM＝4，OQ＝1，求证：CN⊥OB．
（2）当点N在边OB上运动时，四边形OMPQ始终保持为菱形．
①问：－的值是否发生变化？如果变化，求出其取值范围；如果不变，请说明理由．
②设菱形OMPQ的面积为S₁，△NOC的面积为S₂，求的取值范围．

已知点A（－2，n）在抛物线上．
（1）若b＝1，c＝3，求n的值；
（2）若此抛物线经过点B（4，n），且二次函数的最小值是－4，请画出点P（，）的纵坐标随横坐标变化的图象，并说明理由．

某工厂现有甲种原料380千克，乙种原料290千克，计划用这两种原料生产A，B两种产品共50件，已知生产1件A种产品需甲种原料9千克，乙种原料3千克，可获利700元；生产1件B种产品需甲种原料4千克，乙种原料10千克，可获利1200元，设工厂生产A，B两种产品可获总利润是y元，其中甲种产品的生产件数是x，
（1）写出y与x之间的函数关系式；
（2）如何安排A，B两种产品的生产件数，使总利润y有最大值，并求出y的最大值。

动手实验：利用矩形纸片（如图1）剪出一个正六边形纸片；再利用这个正六边形纸片做一个无盖的正六棱柱（棱柱底面为正六边形），如图2．

（1）做一个这样的正六棱柱所需最小的矩形纸片的长与宽的比为多少？
（2）在（1）的条件下，当矩形的长为2a时，要使无盖正六棱柱侧面积最大，正六棱柱的高为多少？并求此时矩形纸片的利用率为多少？（矩形纸片的利用率＝．）