初中数学二次函数在给定区间上的最值解答题

如图，已知一次函数的图象与轴交于点A，与二次函数的图象交于轴上的一点B，二次函数的图象与轴只有唯一的交点C，且OC=2．

求二次函数的解析式；
设一次函数的图象与二次函数的图象的另一交点为D，已知P为轴上的一个动点，且△PBD为直角三角形，求：点P的坐标．

如图，某农户想利用自家院子一面墙和20米长的篱笆围成一个矩形养鸡场，并留出一个1米宽的口子用来进出．
若围成的养鸡场面积为，求围成的养鸡场的长和宽；
请用配方法，求出能围成的矩形养鸡场的最大面积，并说明设计方案．

如图，抛物线与x轴交于A、B两点，与y轴交于C点，四边形OBHC为矩形，CH的延长线交抛物线于点D（5，2），连结BC、AD.

求C点的坐标及抛物线的解析式；
将△BCH绕点B按顺时针旋转90°后再沿x轴对折得到△BEF（点C与点E对应），判断点E是否落在抛物线上，并说明理由；
设过点E的直线交AB边于点P，交CD边于点Q. 问是否存在点P，使直线PQ分梯形ABCD的面积为1∶3两部分？若存在，求出P点坐标；若不存在，请说明理由

如图，四边形ABCD是平行四边形，AB=4，OB=2，抛物线过A、B、C三点，与x轴交于另一点D．一动点P以每秒1个单位长度的速度从B点出发沿BA向点A运动，运动到点A停止，同时一动点Q从点D出发，以每秒3个单位长度的速度沿DC向点C运动，与点P同时停止．

求抛物线的解析式；
若抛物线的对称轴与AB交于点E，与x轴交于点F，当点P运动时间t为何值时，四边形POQE是等腰梯形？
当t为何值时，以P、B、O为顶点的三角形与以点Q、B、O为顶点的三角形相似？

某企业获准生产“上海世博会”纪念徽章，若生产A种款式的纪念徽章125件，B种款式的纪念徽章150件，需生产成本700元；若生产A种款式的纪念徽章100件，B种款式的纪念徽章450件，需生产成本1550元．已知A、B两种纪念徽章的市场零售价分别为2.3元，3.5元
求每个A、B两种款式的纪念徽章的成本是多少元？
随着上海世博会的开幕，为了满足市场的需要，该企业现在每天要生产A、B两种款式的纪念徽章共4500件，若要求每天投入成本不超过10000元，并且每天生产的B种款式的纪念徽章不少于A种款式纪念徽章的．那么每天最多获利多少元，最少获利多少元？获利最多的方案如何设计？

如图，已知二次函数y= -x²+bx+3的图象与x轴的一个交点为A(4,0)，与y轴交于点B.
求此二次函数关系式和点B的坐标；
在x轴的正半轴上是否存在点P，使得△PAB是以AB为底的等腰三角形？若存在，求出点P的坐标；若不存在，请说明理由.

如图，面积为39的直角梯形OABC的直角顶点C在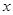轴上，点C坐标为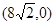，AB=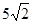，点D是AB边上的一点，且AD：BD=2︰3．有一45°的角的顶点E在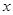轴上运动，角的一边过点D，角的另一边与直线OA交于点F(点D、E、F按顺时针排列),连结DF.设CE=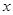，OF=.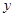

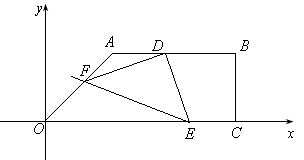
（1）求点D的坐标及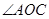的度数；
（2）若点E在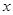轴正半轴上运动，求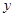与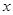的函数关系式；
（3）在点E的运动过程中，是否存在某一时刻，使得△DEF成为等腰三角形？若存在，请求出所有符合条件的点F的坐标；若不存在，请说明理由．

如图，在平面直角坐标系中，等腰直角三角形OMN的斜边ON在x轴上，顶点M的坐标为(3，3)，MH为斜边上的高．过N点垂直于x轴的直线与抛物线y=" -" 4x点D．直线OD的解析式为，点P(x，o)是x轴上一动点，过点P作y轴的平行线，交射线OM与点E．

直接写出点D的坐标及n的值
判断抛物线的顶点是否在直线OM上？并说明理由
设以M、E、H、N为顶点的四边形的面积为S．当x≠3[时，求S与x的函数关系式．

如图，把…张长10cm，宽8cm的矩形硬纸枥的四周各剪去一个同样大小的正方形，再折合成一个无盖的长方体盒子（纸板的厚度忽略不计）．
要使长方体盒子的底面积为48cm²，那么剪去的正方形的边长为多少？
你感到折合而成的长方体盒子的侧面积（不含底面）会不会有最大的情况？如果有，请你求出最大值和此时剪去的正方形的边长；如果没有，请你说明理由

已知抛物线y＝ax²＋x＋2.
当a＝－1时，求此抛物线的顶点坐标和对称轴
若代数式－x²＋x＋2的值为正整数，求x的值；
若a是负数时，当a＝a₁时，抛物线y＝ax²＋x＋2与x轴的正半轴相交于点M(m，0)；当a＝a₂时，抛物线y＝ax²＋x＋2与x轴的正半轴相交于点N(n，0). 若点M在点N的左边，试比较a₁与a₂的大小.

已知：如图，在平面直角坐标系中，矩形OABC的边OA在轴的正半轴上，OC在轴的正半轴上，OA=2，OC=3。过原点O作∠AOC的平分线交AB于点D，连接DC，过点D作DE⊥DC，交OA于点E。

（1）求过点E、D、C的抛物线的解析式；
（2）将∠EDC绕点D按顺时针方向旋转后，角的一边与轴的正半轴交于点F，另一边与线段OC交于点G。如果DF与（1）中的抛物线交于另一点M，点M的横坐标为，那么EF=2GO是否成立？若成立，请给予证明；若不成立，请说明理由；
（3）对于（2）中的点G，在位于第一象限内的该抛物线上是否存在点Q，使得直线GQ与AB的交点P与点C、G构成的△PCG是等腰三角形？若存在，请求出点Q的坐标；若不存在，请说明理由。 

如图，抛物线与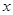轴交于A、B两点，与y轴交于C点，且．

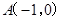求抛物线的解析式及顶点D的坐标；
点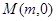是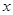轴上的一个动点，当的值最小
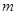时，求的值．

已知：抛物线y＝－x²＋2x＋m-2交y轴于点A（0，2m-7）．与直线
y＝x交于点B、C（B在右、C在左）．
求抛物线的解析式
设抛物线的顶点为E，在抛物线的对称轴上是否存在一点F，使得，若存在，求出点F的坐标，若不存在，说明理由
射线OC上有两个动点P、Q同时从原点出发，分别以每秒个单位长度、每秒2个单位长度的速度沿射线OC运动，以PQ为斜边在直线BC的上方作直角三角形PMQ（直角边分别平行于坐标轴），设运动时间为t秒，若△PMQ与抛物线y＝－x²＋2x＋m-2有公共点，求t的取值范围．

如图，Rt△AOC中，∠ACO=90°，∠AOC=30°．将Rt△AOC绕OC中点E按顺时针方向旋转180°后得到Rt△BCO，BO、CO恰好分别在y轴、x轴上．再将Rt△BCO沿y轴对折得到Rt△BDO．取BC中点F，连接DF，交AB于点G，将△BDG沿DF对折得到△KDG．直线DK交AB于点H．

填空：CE:ED=________,AB:AC=__________；
若BH=，求直线BD解析式
在（2）的条件下，一抛物线过点D、点E、点B，此抛物线位于直线BD上方有一动点Q,△BDQ的面积有无最大值？若有，请求出点Q的坐标；若无，请说明理由

某商场销售一种进价为每件20元的护眼台灯．销售过程中发现，每月销售量y（件）与销售单价x（元）之间的关系可近似的看作一次函数：y=－10x+500．
设商场每月获得利润为w（元），当销售单价定为多少元时，每月可获得最大利润？
若物价部门规定，这种护眼台灯的销售单价不得高于32元，求该商场每月可获得最大利润．