初中数学二次函数在给定区间上的最值解答题

如图，在平面直角坐标系中，已知二次函数的图像与轴交于点，与轴交于A、B两点，点B的坐标为
求二次函数的解析式及顶点D的坐标；
点M是第二象限内抛物线上的一动点，若直线OM把四边形ACDB分成面积为1:2的两部分，求出此时点的坐标；
点P是第二象限内抛物线上的一动点，问：点P在何处时△的面积最大？最大面积是多少？并求出 此时点P的坐标.
                                     

已知关于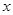的方程．
若方程有两个不相等的实数根，求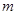的取值范围；
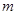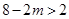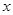若正整数满足，设二次函数的图象与轴交于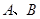两点，将此图象在x轴下方的部分沿x轴翻折，图象的其余部分保持不变，得到一个新的图象．请你结合这个新的图象回答：当直线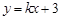与此图象恰好有三个公共点时，求出的值（只需要求出两个满足题意的k值即可）．

在平面直角坐标系中，抛物线经过A（－3,0）、B（4,0）两点，且与y轴交于点C，点D在x轴的负半轴上，且BD＝BC，有一动点P从点A出发，沿线段AB以每秒1个单位长度的速度向点B移动，同时另一个动点Q从点C出发，沿线段CA以某一速度向点A移动.

求该抛物线的解析式；
若经过t秒的移动，线段PQ被CD垂直平分，求此时t的值；
该抛物线的对称轴上是否存在一点M，使MQ＋MA的值最小？若存在，求出点M的坐标；若不存在，请说明理由.

已知二次函数．
当c＝－3时，求出该二次函数的图象与x轴的交点坐标；
若－2＜x＜1时，该二次函数的图象与x轴有且只有一个交点，求c的取值范围．

如图，已知点A (0，4) 和点B (3，0)都在抛物线上．

（1）求、n；
（2）向右平移上述抛物线，记平移后点A的对应点为D，点B的对应点为C，若四边形A BCD为菱形，求平移后抛物线的表达式；
（3）记平移后抛物线的对称轴与直线AC的交点为点E，试在轴上找点F，使得以点C、E、F为顶点的三角形与△    ABE相似。

如图,已知点A (-2,4) 和点B (1,0)都在抛物线y=mx²+2mx+n上．

（1）求m、n值；
（2）向右平移上述抛物线,记平移后点A的对应点为A′,点B的对应点为B′,若四边形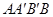为菱形,求平移后抛物线的表达式；
（3）试求出菱形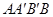的对称中心点M的坐标．

已知：一次函数y=的图象与x轴、y轴的交点分别为B、C，二次函数的关系式为y=ax²-3ax-4a(a<0).

⑴说明：二次函数的图象过B点，并求出二次函数的图象与x轴的另一个交点A的坐标；⑵若二次函数图象的顶点，在一次函数图象的下方，求a的取值范围；
⑶若二次函数的图象过点C，则在此二次函数的图象上是否存在点D，使得△ABD是直角三角形，若存在，求出所有满足条件的点D坐标；若不存在，请说明理由.

如图1，已知正方形OABC的边长为2，顶点A、C分别在x、y轴的正半轴上，M是BC的中点．P(0，m)是线段OC上一个动点(点C除外)，直线PM交AB的延长线于点D．
求点D的坐标(用含m的代数式表示)；
当△ADP是等腰三角形时，求m的值；
设过点P、M、B的抛物线与x轴的正半轴交于点E，过点O作直线ME的垂线，垂足为H(如图2)．当点P从原点O向点C运动时，点H也随之运动．请直接写出点H所经过的路径长(不写解答过程)．

如图，已知点A(−3，5)在抛物线y=x²+c的图象上，点P从抛物线的顶点Q出发，沿y轴以每秒1个单位的速度向正方向运动，连结AP并延长，交抛物线于点B，分别过点A、B作x轴的垂线，垂足为C、D，连结AQ、BQ．
求抛物线的解析式；
当A、Q、B三点构成以AQ为直角边的直角三角形时，求点P离开点Q多少时间？
试探索当AP、AC、BP、BD与一个平行四边形的四条边对应相等（即这四条线段能构成平行四边形）时，点P离开点Q的时刻．

已知二次函数y=ax²+bx+2，它的图像经过点（1，2）．
如果用含a的代数式表示b，那么b=     ；
如图所示，如果该图像与x轴的一个交点为（－1，0）．
① 求二次函数的表达式，并写出图像的顶点坐标；
②在平面直角坐标系中，如果点P到x轴与y轴的距离相等，则称点P为等距点．求出这个二次函数图像上所有等距点的坐标．
当a取a₁,a₂时，二次函数图像与x轴正半轴分别交于点M（m，0），点N（n，0）．如果点N在点M的右边，且点M和点N都在点（1，0）的右边．试比较a₁和a₂的大小．

如图，在平面直角坐标系中，直线与轴交于点，与轴交于点，抛物线经过三点．
求过三点抛物线的解析式并求出顶点的坐标；v
在抛物线上是否存在点，使为直角三角形，若存在，直接写出点
坐标；若不存在，请说明理由；v
试探究在直线上是否存在一点，使得的周长最小，若存在，求
出点的坐标；若不存在，请说明理由．

已知抛物线．
试说明：无论m为何实数，该抛物线与x轴总有两个不同的交点；
如图，当抛物线的对称轴为直线x=3时，抛物线的顶点为点C，直线y=x﹣1与抛物线交于A、B两点，并与它的对称轴交于点D．
①抛物线上是否存在一点P使得四边形ACPD是正方形？若存在，求出点P的坐标；若不存在，说明理由；
②平移直线CD，交直线AB于点M，交抛物线于点N，通过怎样的平移能使得以C、D、M、N为顶点的四边形是平行四边形？（直接写出平移的方法，不要说明理由）

如图，抛物线与x轴交于A，0两点，将抛物线向上移动4个单位长度后得到一条新抛物线，它的顶点在x轴上，新抛物线上的D，E两点分别是A，O两点平移后的对应点。设两条抛物线、线段AD和线段OE围成的面积为S。P（m，n）是新抛物线上一个动点，切满足

⑴求新抛物线的解析式。
⑵当m=-2时，点F的坐标为，试判断直线DF与AE的位置关系，并说明理由。
⑶当的值最小时，求△AEP的面积与S的数量关系。

二次函数的图像交y轴于C点，交轴于A，B两点（点A在点B的左侧），点A、点B的横坐标是一元二次方程的两个根.（1）求出点A、点B的坐标及该二次函数表达式.

（2）如图2，连接AC、BC，点Q是线段OB上
一个动点（点Q不与点O、B重合），过点Q作QD∥AC交于BC点D，设Q点坐标（m，0），当面积S最大时，求m的值.
（3）如图3，线段MN是直线y=x上的动线段（点M在点N左侧），且，若M点的横坐标为n，过点M作x轴的垂线与x轴交于点P，过点N作x轴的垂线与抛物线交于点Q.以点P，M，Q，N为顶点的四边形能否为平行四边形？若能，请求出n的值；若不能，请说明理由．

某企业信息部进行市场调研发现：信息一：如果单独投资A种产品，所获利润y_Ａ(万元)与投资金额x(万元)之间存在某种关系的部分对应值如下表：

x(万元)	1	2	2.5	3	5
yＡ(万元)	0.4	0.8	1	1.2	2

信息二：如果单独投资B种产品，则所获利润y_Ｂ(万元)与投资金额x(万元)之间存在二次函数关系：y_Ｂ＝ax²+bx，且投资2万元时获利润2.4万元，当投资4万元时，可获利润3.2万元．
(1)求出y_Ｂ与x的函数关系式．
(2)从所学过的一次函数、二次函数、反比例函数中确定哪种函数能表示y_Ａ与x之间的关系，并求出y_Ａ与x的函数关系式．
(3)如果企业同时对A、B两种产品共投资15万元，请设计一个能获得最大利润的投资方案，并求出按此方案能获得的最大利润是多少？