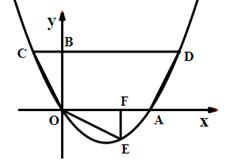
如图,已知平面直角坐标系 中,点A(2,m),B(-3,n)为两动点,其中m﹥1,连结
中,点A(2,m),B(-3,n)为两动点,其中m﹥1,连结 ,
, ,作
,作 轴于
轴于 点,
点, 轴于
轴于 点.
点.
求证:mn=6
当
 时,抛物线经过
时,抛物线经过 两点且以
两点且以 轴为对称轴,求抛物线对应的二次函数的关系式
轴为对称轴,求抛物线对应的二次函数的关系式在(2)的条件下,设直线
 交
交 轴于点
轴于点 ,过点
,过点 作直线
作直线 交抛物线于
交抛物线于 两点,问是否存在直线
两点,问是否存在直线 ,使S⊿POF:S⊿QOF=1:2?若存在,求出直线
,使S⊿POF:S⊿QOF=1:2?若存在,求出直线 对应的函数关系式;若不存在,请说明理由.
对应的函数关系式;若不存在,请说明理由.
如图, 已知抛物线 与y轴相交于C,与x轴相交于A、B,点A的坐标为(-1,0),点C的坐标为(0,-3),抛物线的顶点为D.
与y轴相交于C,与x轴相交于A、B,点A的坐标为(-1,0),点C的坐标为(0,-3),抛物线的顶点为D.求抛物线的解析式和顶点D的坐标
二次函数的图像上是否存在点P,使得S△PAB=8S△ABD?若存在,求出P点坐标;若不存在,请说明理由;
若抛物线的对称轴与x轴交于E点,点F在直线BC上,点M在的二次函数图像上,如果以点F、M、D、E为顶点的四边形是平行四边形,请你求出符合条件的点M的坐标.

在平面直角坐标系中,抛物线 与
与 轴交于A、B两点(点A在点B的左侧),与
轴交于A、B两点(点A在点B的左侧),与 轴交于点C,点B的坐标为(3,0),将直线
轴交于点C,点B的坐标为(3,0),将直线 沿
沿 轴向上平移3个单位长度后恰好经过B、C两点 .
轴向上平移3个单位长度后恰好经过B、C两点 .

求直线BC及抛物线的解析式
设抛物线的顶点为D,点P在抛物线的对称轴上,且∠APD=∠ACB,求点P的坐标;
连结CD,求∠OCA与∠OCD两角度数的和
如图,在平面直角坐标系xOy中,抛物线 与y轴交于点B,过点B作x轴的平行线BC,交抛物线于点C,连接AC.现有两动点P,Q分别从0,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动,线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x辅于点F.设动点P,Q移动的时间为t(单位:秒).
与y轴交于点B,过点B作x轴的平行线BC,交抛物线于点C,连接AC.现有两动点P,Q分别从0,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动,线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x辅于点F.设动点P,Q移动的时间为t(单位:秒).求A,B,C三点的坐标和抛物线的顶点坐标;
当O<t<
 时’△PQF的面积是否为定值?若是,求出此定值,若不是,说明理由
时’△PQF的面积是否为定值?若是,求出此定值,若不是,说明理由当t为何值时,△PQF为等腰三角形?请写出解答过程.

如图,抛物线 过原点O,与x轴交于A,点D(4,2)在该抛物线上,过点D作CD∥x轴,交抛物线于点C,交y轴于点B,连结CO、AD.
过原点O,与x轴交于A,点D(4,2)在该抛物线上,过点D作CD∥x轴,交抛物线于点C,交y轴于点B,连结CO、AD.求抛物线的解析式及点C的坐标
将△BCO绕点O按顺时针旋转90°后 再沿x轴对折得到△OEF(点C与点E对应),判断点E是否落在抛物线上,并说明理由;
设过点E的直线交OA于点P,交CD边于点Q. 问是否存在点P,使直线PQ分梯形AOCD的面积为1∶3两部分?若存在,求出P点坐标;若不存在,请说明理由.
如图23,已知抛物线 与
与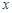 轴相交于A、B两点,其对称轴为直线
轴相交于A、B两点,其对称轴为直线 ,且与x轴交于点D,AO=1.
,且与x轴交于点D,AO=1.填空:
 =_______。
=_______。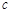 =_______,点B的坐标为(_______,_______):
=_______,点B的坐标为(_______,_______):若线段BC的垂直平分线EF交BC于点E,交
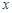 轴于点F.求FC的长;
轴于点F.求FC的长;探究:在抛物线的对称轴上是否存在点P,使⊙P与
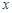 轴、直线BC都相切?若存在,请求出点P的坐标;若不存在,请说明理由。
轴、直线BC都相切?若存在,请求出点P的坐标;若不存在,请说明理由。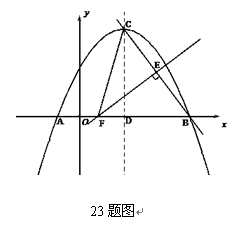
如图(1),分别以两个彼此相邻的正方形OABC与CDEF的边OC、OA所在直线为 轴、
轴、 轴建立平面直角坐标系(O、C、F三点在x轴正半轴上).若⊙P过A、B、E三点(圆心在
轴建立平面直角坐标系(O、C、F三点在x轴正半轴上).若⊙P过A、B、E三点(圆心在 轴上)交y轴于另一点Q,抛物线
轴上)交y轴于另一点Q,抛物线 经过A、C两点,与
经过A、C两点,与 轴的另一交点为G,M是FG的中点,B点坐标为(2,2).
轴的另一交点为G,M是FG的中点,B点坐标为(2,2).求抛物线的函数解析式和点E的坐标;
求证:ME是⊙P的切线;

如图9, 已知抛物线与 轴交于A (-4,0) 和B(1,0)两点,与
轴交于A (-4,0) 和B(1,0)两点,与 轴交于C(0,-2)点.
轴交于C(0,-2)点.求此抛物线的解析式;
设G是线段BC上的动点,作GH//AC交AB于H,连接CF,当△BGH的面积是△CGH面积的3倍时,求H点的坐标;
若M为抛物线上A、C两点间的一个动点,过M作
 轴的平行线,交AC于N,当M点运动到什么位置时,线段MN的值最大,并求此时M点的坐标
轴的平行线,交AC于N,当M点运动到什么位置时,线段MN的值最大,并求此时M点的坐标
如图,在平面直角坐标系中放置一矩形ABCO,其顶点为A(0,1)、B(-3,1)、C(-3,0)、O(0,0).将此矩形沿着过E(-,1)、
F(-,0)的直线EF向右下方翻折,B、C的对应点分别为B′、C′.
|
如图,抛物线 与
与 轴相交于
轴相交于 、
、 两点(点
两点(点 在点
在点 的左侧),与
的左侧),与 轴相交于点
轴相交于点 ,顶点为
,顶点为 .
.
直接写出
 、
、 、
、 三点的坐标和抛物线的对称轴;
三点的坐标和抛物线的对称轴;连接
 ,与抛物线的对称轴交于点
,与抛物线的对称轴交于点 ,点
,点 为线段
为线段 上的一个动点,过点
上的一个动点,过点 作
作 交抛物线于点
交抛物线于点 ,设点
,设点 的横坐标为
的横坐标为 ;
;
①用含 的代数式表示线段
的代数式表示线段 的长,并求出当
的长,并求出当 为何值时,四边形
为何值时,四边形 为平行四边形?
为平行四边形?
②设 的面积为
的面积为 ,求
,求 与
与 的函数关系式.
的函数关系式.
如图,二次函数 与x轴交于A、B两点,与y轴交于C点,点P从A点出发,以1个单位每秒的速度向点B运动,点Q同时从C点出发,以相同的速度向y轴正方向运动,运动时间为t秒,点P到达B点时,点Q同时停止运动。设PQ交直线AC于点
与x轴交于A、B两点,与y轴交于C点,点P从A点出发,以1个单位每秒的速度向点B运动,点Q同时从C点出发,以相同的速度向y轴正方向运动,运动时间为t秒,点P到达B点时,点Q同时停止运动。设PQ交直线AC于点
(1)求直线AC的解析式;
(2)设△PQC的面积为S,求S关于t的函数解析式;
(3)在y轴上找一点M,使△MAC和△MBC都是等腰三角形。直接写出所有满足条件的M点的坐标;
(4)过点P作PE⊥AC,垂足为E,当P点运动时,线段EG的长度是否发生改变,请说明理由。
如图,在平面直角坐标系 中,抛物线
中,抛物线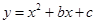 与
与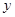 轴交于点
轴交于点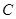 ,与
,与 轴交于
轴交于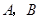 两点,点
两点,点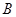 的坐标为
的坐标为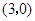 ,直线
,直线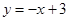 恰好经过B、C两点.
恰好经过B、C两点.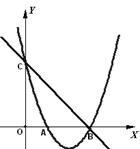
(1)写出点C的坐标;
(2)求出抛物线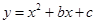 的解析式,并写出抛物线的对称轴和点
的解析式,并写出抛物线的对称轴和点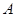 的坐标;
的坐标;
(3)点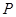 在抛物线的对称轴上,抛物线顶点为D且
在抛物线的对称轴上,抛物线顶点为D且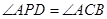 ,求点
,求点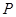 的坐标.
的坐标.
已知抛物线L:
(1)证明:不论k取何值,抛物线L的顶点C总在抛物线 上;
上;
(2)已知 时,抛物线L和x轴有两个不同的交点A、B,求A、B间距取得最大值时k的值;
时,抛物线L和x轴有两个不同的交点A、B,求A、B间距取得最大值时k的值;
(3)在(2)A、B间距取得最大值条件下(点A在点B的右侧),直线y=ax+b是经过点A,且与抛物线L相交于点D的直线. 问是否存在点D,使△ABD为等边三角形,如果存在,请写出此时直线AD的解析式;如果不存在,请说明理由.
已知抛物线 =
= +
+ +
+ -4.
-4.
(1)当 =2时,求出此抛物线的顶点坐标;
=2时,求出此抛物线的顶点坐标;
(2)求证:无论 为什么实数,抛物线都与
为什么实数,抛物线都与 轴有交点,且经过
轴有交点,且经过 轴上的一定点;
轴上的一定点;
(3)已知抛物线与 轴交于A(
轴交于A( 1,0)、B(
1,0)、B( 2,0)两点(A在B的左边),|
2,0)两点(A在B的左边),| 1|<|
1|<| 2|,与
2|,与 轴交于C点,且S△ABC=15.问:过A,B,C三点的圆与该抛物线是否有第四个交点?试说明理由.如果有,求出其坐标.
轴交于C点,且S△ABC=15.问:过A,B,C三点的圆与该抛物线是否有第四个交点?试说明理由.如果有,求出其坐标.
试题篮
()