初中数学二次函数在给定区间上的最值解答题

已知二次函数y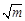＝x²+(3-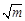)x-3(m>0)的图象与x轴交于点 (x₁, 0)和(x₂, 0),
且x₁<x₂.
（1）求x₂的值;
（2）求代数式的值.

某商店销售一种进价为20元/双的手套，经调查发现，该种手套每天的销售量w(双)
与销售单价x(元)满足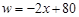(20≤x≤40),设销售这种手套每天的利润为y（元）.
（1）求y与x之间的函数关系式；
（2）当销售单价定为多少元时, 每天的利润最大？最大利润是多少？

李经理在某地以10元/千克的批发价收购了2 000千克核桃，并借一仓库储存．在存放过程中，平均每天有6千克的核桃损耗掉，而且仓库允许存放时间最多为60天．若核桃的市场价格在批发价的基础上每天每千克上涨0.5元。
（1）存放x天后，将这批核桃一次性出售，如果这批核桃的销售总金额为y元，试求出y与x之间的函数关系式；
（2）如果仓库存放这批核桃每天需要支出各种费用合计340元，李经理要想获得利润22 500元，需将这批核桃存放多少天后出售？（利润＝销售总金额－收购成本－各种费用）

已知二次函数.
（1）求它的对称轴与轴交点D的坐标；
（2）将该抛物线沿它的对称轴向上平移，如图所示，设平移后的抛物线的顶点为，与轴、轴的交点分别为A、B、C三点，连结AC、BC,若∠ACB=90°.
①求此时抛物线的解析式；
②以AB为直径作圆，试判断直线CM与此圆的位置关系，并说明理由.
 

.已知均为整数，直线与三条抛物线和交点的个数分别是2,1,0，若

如图，抛物线y =ax²+bx+c过点A（-1，0），且经过直线y =x-3与x轴的交点B及与y轴的交点C．

（1）求点B、C的坐标；
（2）求抛物线的解析式；   
（3）求抛物线的顶点M的坐标；
（4）在直线y =x-3上是否存在点P，使△CMP是等腰三角形？若存在，求出满足条件的P点坐标；若不存在，说明理由．

某大学校园内一商店，销售一种进价为每件20元的台灯．销售过程中发现，每月销售量（件）与销售单价（元）之间的关系可近似的看作一次函数：．
（1）设此商店每月获得利润为（元），当销售单价定为多少元时，每月可获得最大利润？【利润=（销售单价-进价）×销售量】
（2）如果此商店想要每月获得2000元的利润，那么销售单价应定为多少元？
（3）根据物价部门规定，这种台灯的销售单价不得高于32元，如果此商店想要每月获得的利润不低于2000元，那么商店每月的成本最少需要多少元？【成本＝进价×销售量】

如图，四边形是平行四边形，抛物线过三点，与轴交于另一点.一动点以每秒1个单位长度的速度从点出发沿向点运动，运动到点停止，同时一动点从点出发，以每秒3个单位长度的速度沿向点运动，与点同时停止.
 
（1）求抛物线的解析式；
（2）若抛物线的对称轴与交于点，与轴交于点，当点运动时间为何值时，四边形是等腰梯形？
（3）当为何值时，以为顶点的三角形与以点为顶点的三角形相似？

如图，在平面直角坐标系中，以点C（1，1）为圆心，2为半径作圆，交轴于两点，开口向下的抛物线经过点，且其顶点在⊙上．

（1）求的大小；
（2）写出两点的坐标；
（3）试确定此抛物线的解析式；
（4）在该抛物线上是否存在一点，使线段与互相平分？若存在，求出点的坐标；若不存在，请说明理由．

已知：如图，正方形纸片ABCD的边长是4，点M、N分别在两边AB和CD上（其中点N不与点C重合），沿直线MN折叠该纸片，点B恰好落在AD边上点E处．

（1）设AE＝x，四边形AMND的面积为 S，求 S关于x 的函数解析式，并指明该函数的定义域；
（2）当AM为何值时，四边形AMND的面积最大？最大值是多少？
（3）点M能是AB边上任意一点吗？请求出AM的取值范围．  

已知：如图，在平面直角坐标系中，边长为的等边随着顶点A在抛物线上运动而运动，且始终有BC∥x轴．

（1）当顶点A运动至与原点重合时，顶点C是否在该抛物线上？
（2）在运动过程中有可能被x轴分成两部分，当上下两部分的面积之比为1∶8（即）时，求顶点A的坐标；
（3）在运动过程中，当顶点B落在坐标轴上时，直接写出顶点C的坐标．

已知：关于x的一元一次方程kx=x+2 ①的根为正实数，二次函数y=ax²−bx+kc（c≠0）的图象与x轴一个交点的横坐标为1．
（1）若方程①的根为正整数，求整数k的值；
（2）求代数式的值；
（3）求证：关于x的一元二次方程ax²−bx+c="0" ②必有两个不相等的实数根．

已知：如图，抛物线与轴交于点，点，与直线相交于点，点，直线与轴交于点．

（1）求的面积．
（2）若点在线段上以每秒1个单位长度的速度从向运动（不与重合），同时，点在射线上以每秒2个单位长度的速度从向运动．设运动时间为秒，请写出的面积与的函数关系式，并求出点运动多少时间时，的面积最大，最大面积是多少？

如图，Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上，O为坐标原点，A、B两点的坐标分别为（，0）、（0，4），抛物线经过B点，且顶点在直线上．

（1）求抛物线对应的函数关系式；
（2）若△DCE是由△ABO沿x轴向右平移得到的，当四边形ABCD是菱形时，试判断点C和点D是否在该抛物线上，并说明理由；
（3）若M点是CD所在直线下方该抛物线上的一个动点，过点M作MN平行于y轴交CD于点N．设点M的横坐标为t，MN的长度为l．求l与t之间的函数关系式，并求l取最大值时，点M的坐标．

在平面直角坐标系xOy中,反比例函数的图象与抛物线 
交于点A(3, n).
求n的值及抛物线的解析式；
过点A作直线BC，交x轴于点B，交反比例函数（）的图象于点C，且AC=2AB，求B、C两点的坐标；                        
在（2）的条件下，若点P是抛物线对称轴上的一点，且点P到x轴和直线BC的距离相等，求点P的坐标.