初中数学二次函数在给定区间上的最值解答题

今年我国多个省市遭受严重干旱，受旱灾的影响，4月份，我市某蔬菜价格呈上升趋势，其前四周每周的平均销售价格变化如下表：

周数x	1	2	3	4
价格y（元/千克）	2	2.2	2.4	2.6

（1）请观察题中的表格，用所学过的一次函数、反比例函数或二次函数的有关知识直接写出4月份y与x 的函数关系式；
（2）进入5月，由于本地蔬菜的上市，此种蔬菜的平均销售价格y（元/千克）从5月第1周的2.8元/千克下降至第2周的2.4元/千克，且y与周数x的变化情况满足二次函数y＝－ x²＋bx＋c. ，请求出5月份y与x的函数关系式
（3）若4月份此种蔬菜的进价m（元/千克）与周数x所满足的函数关系为m＝x＋1.2，5月份此种蔬菜的进价m（元/千克）与周数x所满足的函数关系为m＝x＋2．试问4月份与5月份分别在哪一周销售此种蔬菜一千克的利润最大？且最大利润分别是多少？

(本题12分) 某商品每件买入价为30元，销售价的25%用于纳税等其他费用，每日销售量P件与销售价x元之间满足关系式：P=-x+100(40＜x＜100).
（1）当销售价为60元时，每件商品的纯利润为      元，此时每日销售量为      件.
（2）若要使每件商品的纯利润y元保持在买入价的20%--70%（包括20%和70%），问该如何确定销售价？，并求出最大利润. [总利润=每件纯利润×销售量]

（本小题10分）
如图，抛物线与x轴交与A(1,0),B(- 3，0)两点，
（1）求该抛物线的解析式；
（2）抛物线交y轴与C点，在该抛物线的对称轴上是否存在点Q，使得△QAC的周长最小？若存在，求出Q点的坐标；若不存在，请说明理由.

已知二次函数y= x² -4x+3.
（1）用配方法将y= x² - 4x+3化成y=a (x-h) ² +k的形式；
（2）在平面直角坐标系中，画出这个二次函数的图象；
（3）写出当x为何值时，y>0．
（4）写出当时，直接写出相应y的取值范围.

如图，对称轴为的抛物线与轴相交于点、.

求抛物线的解析式，并求出顶点的坐标；
连结AB，把AB所在的直线平移，使它经过原点O，得到直线l.点P是l上一动点.设以点A、B、O、P为顶点的四边形面积为S，点P的横坐标为，当0＜S≤18时，求的取值范围；
在（2）的条件下，当取最大值时，抛物线上是否存在点，使△OP为直角三角形且OP为直角边.若存在,直接写出点的坐标；若不存在，说明理由.

如图，已知抛物线经过原点和轴上另一点，它的对称轴="2" 与轴交于点，直线经过抛物线上一点，且与直线交于点.

求的值及该抛物线的函数关系式；
若点是轴上一动点，当△△∽△时，求点的坐标；
若是该抛物线上的一个动点，是否存在这样的点,使得,若存在，试求出所有符合条件的点P的坐标；若不存在，请说明理由.

已知抛物线y=x+bx+c，经过点A（0，5）和点B（3，2）
（1）求抛物线的解析式：
（2）现有一半径为l，圆心P在抛物线上运动的动圆，问⊙P在运动过程中，是否存在⊙P与坐标轴相切的情况？若存在，请求出圆心P的坐标：若不存在，请说明理由；
（3）若⊙ Q的半径为r，点Q 在抛物线上、⊙Q与两坐轴都相切时求半径r的值

（1）把二次函数y=2x²－8x+6代成的形式.
（2）写出抛物线的顶点坐标、对称轴和最值，并说明该抛物线是由哪一条形如的抛物线经过怎样的变换得到的？
（3）求该抛物线与坐标轴的交点坐标。

已知：二次函数的解析式。
（1）求这个二次函数的顶点坐标；
（2）求这个二次函数图象与x轴的交点坐标；
（3）当x取何值时，随x的增大而增大；
（4）如图，若直线的图象与该二次图象交于A（，），B（2，n）两点，结合图象直接写出当x取何值时？

A（1，0），B（3，0）。

（1）求抛物线的解析式；


所有点P的坐标；
（3）设抛物线交y轴于点C，问该抛物线对称轴上是否存在点M，使得△MAC的周长最小。若存在，求出点M的坐标；若不存在，请说明理由。

有研究发现，人体在注射一定剂量的某种药物后的数小时内，体内血液中的药物浓度（即血药浓度）y毫克/升是时间t（小时）的二次函数，已知某病人的三次化验结果如下表：

（1）求y与t的函数关系式；
（2）在注射后的第几小时，该病人体内的血药浓度达到最大？最大浓度是多少？
（3）该病人在注射后的几个小时内，体内的血药浓度超过0.3毫克/升？

已知二次函数y=ax²＋bx－3的图象经过点A（2，-3），B（-1，0）．
求二次函数的解析式.

已知一元二次方程x²－4x＋3=0的两根是m，n且m＜n.如图12，若抛物线y=-x²+bx
+c的图像经过点A（m，0）、B（0，n）.
求抛物线的解析式.
若（1）中的抛物线与x轴的另一个交点为C.根据图像回答，当x取何值时，抛物线的图像在直线BC的上方？
点P在线段OC上，作PE⊥x轴与抛物线交与点E，若直线BC将△CPE的面积分成相等的两部分，求点P的坐标.

如图, 已知抛物线经过坐标原点O及，其顶点为B(m,3),C是AB中点，
点E是直线OC上的一个动点 (点E与点O不重合)，点D在y轴上, 且EO=ED .

（1）求此抛物线及直线OC的解析式；
（2）当点E运动到抛物线上时, 求BD的长；
（3）连接AD, 当点E运动到何处时，△AED的面积为，请直接写出此时E点的
坐标.

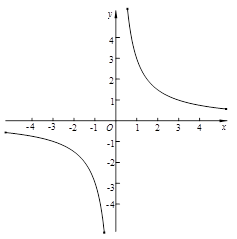
已知二次函数y=ax²+bx+c的图象与反比例函数的图象交于点A (a, -3)，与y轴交于点B.

（1）试确定反比例函数的解析式;
（2）若ÐABO =135°, 试确定二次函数的解析式;
（3）在（2）的条件下,将二次函数y=ax² + bx + c的图象先沿x轴翻折, 再向右平移到与反比例函数的图象交于点P (x₀, 6) . 当x₀≤x≤3时, 求平移后的二次函数y的取值范围.