初中数学二次函数在给定区间上的最值解答题

(14分)如图，抛物线:y＝ax²＋bx+1的顶点坐标为D（1,0），

（1）求抛物线的解析式；
（2）如图1，将抛物线向右平移1个单位，向下平移1个单位得到抛物线，直线，
经过点D交y轴于点A，交抛物线于点B，抛物线的顶点为P,求△DBP的面积；
如图2，连结AP,过点B作BC⊥AP于C,设点Q为抛物线上点至点之间的一动点，
连结 并延长交于点，试问：当点Q运动到什么位置时，△BCF的面积为。

已知在平面直角坐标系中，抛物线与轴相交于，两点，对称轴与轴相交于点，顶点为点，且的正切值为.

（1）求顶点的坐标；
（2）求抛物线的表达式；
（3）点是抛物线上的一点，且位于第一象限，联结，若，求点的坐标.

如图，面积为8的矩形ABOC的边OB、OC分别在轴、轴的正半轴上，点A在双曲线的图象上，且AC=2

求值
将矩形ABOC以B旋转中心，顺时针旋转90°后得到矩形FBDE，双曲线交DE于M点，交EF于N点，求△MEN的面积

如图，二次函数（）的图象与轴交于两点，与轴相交于点．连结两点的坐标分别为、，且当和时二次函数的函数值相等．
（1）求实数的值；
（2）若点同时从点出发，均以每秒1个单位长度的速度分别沿边运动，其中一个点到达终点时，另一点也随之停止运动．当运动时间为秒时，连结，将沿翻折，点恰好落在边上的处，求的值及点的坐标；
（3）在（2）的条件下，二次函数图象的对称轴上是否存在点，使得以为项点的三角形与相似？如果存在，请求出点的坐标；如果不存在，请说明理由．

若⊙P与函数图象有且只有一个公共点，并且与轴、轴都相切的圆，则称⊙P是这个函数的伴圆．
如图1，求的伴圆的圆心P的坐标及半径r；
如图2，⊙P的半径为1，若⊙P是二次函数的伴圆，写出满足要求的开口方向不同的两个二次函数的解析式；
如图3，求一次函数的所有伴圆的圆心P的坐标及半径．

如图，边长为2的等边△OAB在第一象限，写出B点的坐标，并求过O、A、B三点的二次函数的解析式．

如图,已知二次函数的图像过A(2，0)，B（0，-6）两点．

（1）求这个二次函数的解析式；
（2）设该二次函数图像的对称轴与轴的交点C，连接AB，BC，求△ABC的面积．

如图，二次函数y＝ax²－2ax＋的图象与x轴交于A、B二点，与y轴交于C点．抛物线的顶点为E（1，2），D为抛物线上一点，且CD∥x轴．

（1）求此二次函数的关系式；
（2）写出A、B、C、D四点的坐标；
（3）若点F在抛物线的对称轴上，点G在抛物线上，且以A、B、F、G四点为顶点的四边形为平行四边形，求点G 的坐标．

（本小题满分12分）如图，已知抛物线与关于轴对称，并与轴交于点M，与轴交于点A和B.

（1）求出的解析式，试猜想出一般形式关于轴对称的二次函数解析式（不要求证明）；
（2）若AB的中点是C，求；
（3）如果一次函数过点,且与抛物线，相交于另一点，如果 ，且,求的值。

一家计算机专买店A型计算器每只进价12元，售价20元，多买优惠：凡是一次买10只以上的，每多买一只，所买的全部计算器每只就降低0.10元，例如，某人买20只计算器，于是每只降价0.10×（20-10）＝1（元），因此，所买的全部20只计算器都按每只19元的价格购买．但是最低价为每只16元．
（1）求一次至少买多少只，才能以最低价购买？
（2）写出专买店当一次销售x（x＞10）只时，所获利润y元）与x（只）之间的函数关系式，并写出自变量x的取值范围；
（3）一天，甲买了46只，乙买了50只，店主却发现卖46只赚的钱反而比卖50只赚的钱多，你能用数学知识解释这一现象吗？为了不出现这种现象，在其他优惠条件不变的情况下，店家应把最低价每只16元至少提高到多少？

已知抛物线m：y=ax²+bx+c(a ≠ 0) 与x轴交于A、B两点(点A在左)，与y轴交于点C，顶点为M，抛物线上部分点的横坐标与对应的纵坐标如下表：
 
（1）根据表中的各对对应值，请写出三条与上述抛物线m有关（不能直接出现表中各对对应值）的不同类型的正确结论；
（2）若将抛物线m，绕原点O顺时针旋转180°，试写出旋转后抛物线n的解析式,并在坐标系中画出抛物线m、n的草图；
（3）若抛物线n的顶点为N，与x轴的交点为E、F（点E、 F分别与点A、B对应），试问四边形NFMB是何种特殊四边形？并说明其理由．

阅读材料：我们学过二次函数的图像的平移，如：将二次函数y=2x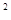的图像沿x轴向左平移3个单位长度得到函数y=2(x+3)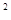的图像，再沿y轴向下平移1个单位长度，得到函数y=2(x+3)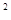-1的图像.
类似的，将一次函数y=2x的图像沿x轴向右平移1个单位长度可得到函数y=2(x-1)的图像，再沿y轴向上平移1个单位长度，得到函数y=2(x-1)+1的图像.
解决问题：
将一次函数y= -x的图像沿x轴向右平移2个单位长度，再沿y轴向上平移3个单位长度，得到函数           的图像；
将y=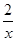的图像沿y轴向上平移3个单位长度，得到函数       的图像，再沿x轴向右平移1个单位长度，得到函数         的图像；
函数y=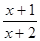的图像可由哪个反比例函数的图像经过怎样的变换得到？

如图所示，抛物线m：y=ax2+b（a＜0，b＞0）与x轴于点A、B（点A在点B的左侧），与y轴交于点C.将抛物线m绕点B旋转180°，得到新的抛物线n，它的顶点为C1，与x轴的另一个交点为A1.

(1)当a=－1 , b=1时，求抛物线n的解析式；
(2)四边形AC1A1C是什么特殊四边形，请写出结果并说明理由；
(3)若四边形AC1A1C为矩形，请求出a和b应满足的关系式.

如图，已知抛物线y＝ax2＋bx＋c(a≠0)的对称轴为x＝1，且抛物线经过A（—1，0）、C（0，—3）两点，与x轴交于另一点B．
（1）求这条抛物线所对应的函数关系式；
（2）在抛物线的对称轴x＝1上求一点M，使点M到点A的距离与到点C的距离之和最小，并求出此时点M的坐标；
（3）设点P为抛物线的对称轴x＝1上的一动点，求使∠PCB＝90°的点P的坐标．

如图，直线y=2x+4与x轴、y轴分别交于A、B两点，把△OAB绕点O顺时针旋转90°得到△OCD．

求经过A、B、D三点的抛物线的解析式
点P是第一象限内抛物线上一点，是否存在这样的点P，使得点P到直线CD的距离最大，若存在，请求出点P的坐标；若不存在，请说明理由．