初中数学二次函数在给定区间上的最值解答题

为了保证春节期间的水果供应，保障水果的无公害，江都“乐天玛特”超市从水果原产地联系了一种水果，根据以往销售经验，估计春节期间，这种水果每天的单价x元与销售量y千克之间有如下的一次函数的关系：

每千克的 售价（元）	41	40	39	38	……
每天的销售量（千克）	50	55	60	65	……

求出y与x的函数关系式.
如果此水果进价为每千克29元，若不考虑其它情况，那么每千克售价定为多少元时，当天所获得的利润最大？最大利润为多少元？

如图1，点C、B分别为抛物线C₁：y₁＝x²＋1，抛物线C₂：y²＝a₂x²＋b₂x＋c₂的顶点．分别过点B、C作x轴的平行线，交抛物线C₁、C₂于点A、D，且AB＝BD．

(1)求点A的坐标：
(2)如图2，若将抛物线C₁：“y₁＝x²＋1”改为抛物线“y₁＝2x²＋b₁x＋c₁”．其他条件不变，求CD的长和a₂的值；
(3)如图2，若将抛物线C₁：“y₁＝x²＋1”改为抛物线“y₁＝4x²＋b₁x＋c₁”，其他条件不变，求b₁＋b₂的值   ▲   （直接写结果）．

在平面直角坐标系中，以点A（3，0）为圆心，5为半径的圆与轴相交于点、（点B在点C的左边），与轴相交于点D、M（点D在点M的下方）．
（1）求以直线x=3为对称轴，且经过D、C两点的抛物线的解析式；
（2）若E为直线x=3上的任一点，则在抛物线上是否存在
这样的点F，使得以点B、C、E、F为顶点的四边形是平
行四边形？若存在，求出点F的坐标；若不存在，说明理由． 

密苏里州圣路易斯拱门是座雄伟壮观的抛物线形的建筑物，是美国最高的独自挺立的纪念碑，如图．拱门的地面宽度为200米，两侧距地面高150米处各有一个观光窗，两窗的水平距离为100米，求拱门的最大高度．

已知二次函数y=x²-2x-3的图象与x轴交于A、B两点

(A在B的左侧)，与y轴交于点C，顶点为D。
(1) 求点A、B、C、D的坐标，并在下面直角坐标系中画出该二次
函数的大致图象；
(2) 说出抛物线y=x²-2x-3可由抛物线y=x²如何平移得到？

已知P（－3，m）和Q(1，m)是抛物线y＝2x²＋bx＋1上的两点．
(1)求b的值；
(2)判断关于x的一元二次方程2x²＋bx＋1＝0是否有实数根，若有，求出它的实数根；若没有，请说明理由；
(3)将抛物线y＝2x²＋bx＋1的图象向上平移k(k是正整数）个单位，使平移后的图象与x轴无交点，求k的最小值．

用长度为20m的金属材料制成如图所示的金属框，下部为矩形，上部为等腰直角三角形，其斜边长为2xm．当该金属框围成的图形面积最大时，图形中矩形的相邻两边长各为多少？请求出金属框围成的图形的最大面积．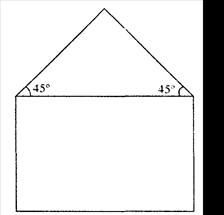

（本题8分）某公司投资新建了一商场，共有商铺30间，据预测，当每间的年租金定为10万元时，可全部租出．每间的年租金每增加5000元，少租出商铺1间．该公司要为租出的商铺每间每年交各种费用1万元，未租出的商铺每问每年交各种费用5000元．
  (1)当每间商铺的年租金定为13万元时，能租出多少间？
(2)当每间商铺的年租金定为多少万元时，该公司的年收益（收益＝租金－各种费用）为275万元？
(3)当每间商铺的年租金定为多少万元时，该公司的年收益最大？（假设年租金每次增加的幅度必须为5000元的倍数）

（本题6分）如图，在平面直角坐标系中，点A，B，C的坐标分别为(0，2)，(3，2)，(2，3)．

(1)请在图中画出△ABC向下平移3个单位的图像△A'B'C'；
(2)若一个二次函数的图象经过(1)中△A'B'C'的三个顶点，求此二次函数的关系式．

（本题6分）已知函数y＝－x²＋2x－．

(1)用配方法求它的顶点坐标；
(2)在平面直角坐标系中画出它的简图：
(3)根据图象回答：x取什么值时，y>0．

（本小题满分12分）
某公司销售一种新型节能产品，现准备从国内和国外两种销售方案中选择一种进行销售．若只在国内销售，销售价格y（元/件）与月销量x（件）的函数关系式为y =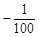x＋150，成本为20元/件，无论销售多少，每月还需支出广告费62500元，设月利润为w_内（元）（利润 = 销售额－成本－广告费）．若只在国外销售，销售价格为150元/件，受各种不确定因素影响，成本为a元/件（a为常数，10≤a≤40），当月销量为x（件）时，每月还需缴纳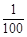x² 元的附加费，设月利润为w_外（元）（利润 = 销售额－成本－附加费）．
（1）当x = 1000时，y =        元/件，w_内 =        元；
（2）分别求出w_内，w_外与x间的函数关系式（不必写x的取值范围）；
（3）当x为何值时，在国内销售的月利润最大？若在国外销售月利润的最大值与在国内销售月利润的最大值相同，求a的值；
（4）如果某月要将5000件产品全部销售完，请你通过分析帮公司决策，选择在国内还是在国外销售才能使所获月利润较大？
参考公式：抛物线的顶点坐标是．

已知：如图，抛物线与轴交于点，点，与直线相交于点，点，直线与轴交于点．

（1）求的面积．
（2）若点在线段上以每秒1个单位长度的速度从向运动（不与重合），同时，点在射线上以每秒2个单位长度的速度从向运动．设运动时间为秒，请写出的面积与的函数关系式，并求出点运动多少时间时，的面积最大，最大面积是多少？

已知抛物线y＝ax+bx+c与轴交于两点，若两点的横坐标分别是一元二次方程的两个实数根，与轴交于点（0，3），
（1）求抛物线的解析式；
（2）在此抛物线上求点，使.

(8分)如图，在平面直角坐标系中，以点为圆心，以2为半径作圆，交轴于两点，开口向下的抛物线经过点，且其顶点在⊙C上．

 
（1）求的大小；
（2）写出A、B两点的坐标；
（3）试确定此抛物线的解析式；
（4）在该抛物线上是否存在一点，使线段与互相平分？若存在，求出点的坐标；若不存在，请说明理由．

王强在一次高尔夫球的练习中，在某处击球，其飞行路线满足抛物线，其中（m）是球的飞行高度，（m）是球飞出的水平距离，结果球离球洞的水平距离还有2m．

（1）请求出球飞行的最大水平距离．
（2）若王强再一次从此处击球，要想让球飞行的最大高度不变且球刚好进洞，则球飞行路线应满足怎样的抛物线，求出其解析式．