初中数学三角形的五心试题

一轮船先向东航行8海里，接着又向北航行6海里，则该船这时离出发点_____海里．

等腰三角形的两边长分别是6和5，则周长是________．

等腰三角形的两个内角的比是1: 2，则这个等腰三角形的顶角的度数是：

A．72°

B．36°或90°

C．36°

D．45°

如图，已知下列条件不能判定≌的是：

A．

B．

C．

D．∥

如图，图中数字表示所在正方形的面积，则字母B所代表的正方形的面积是：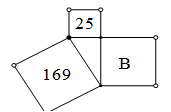

A．196

B．144

C．13

D．12

已知，△ABC是边长为4cm的等边三角形，点P，Q分别从顶点A，B同时出发，沿线段AB，BC运动，且它们的速度均为1cm/s．当点P到达点B时，P、Q两点停止运动．设点P的运动时间为t（s）．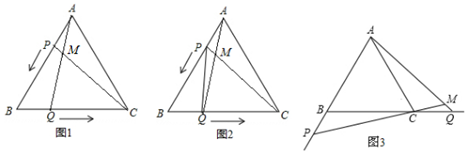

（1）如图1，连接AQ、CP，相交于点M，则点P，Q在运动的过程中，∠CMQ会变化吗？若变化，则说明理由；若不变，请求出它的度数．
（2）如图2，当t为何值时，△PBQ是直角三角形？
（3）如图3，若点P、Q在运动到终点后继续在射线AB、BC上运动，直线AQ、CP交点为M，请直接写出∠CMQ度数．

小明遇到这样一个问题：如图1，在Rt△ABC中，∠ACB=90°，∠A=60°，CD平分∠ACB，试判断BC和AC、AD之间的数量关系．小明发现，利用轴对称做一个变化，在BC上截取CA′=CA，连接DA′，得到一对全等的三角形，从而将问题解决（如图2）．

（1）求证：△ADC≌△A′DC；
（2）试猜想写出BC和AC、AD之间的数量关系，并给出证明．

如图，在△ABC中，P、Q分别是BC、AC上的点，作PR⊥AB，PS⊥AC，垂足分别为R、S，若AQ=PQ，PR=PS，则下列四个结论：①PA平分∠BAC；②AS=AR；③QP∥AR；④△BRP≌△CSP，其中结论正确的的序号为（请将你认为正确的序号都填上）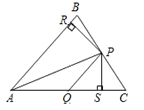

等边的两条角平分线和交于点，则等于_______度．

下列各种说法正确的是

A．面积相等的两个三角形一定全等

B．周长相等的两个三角形一定全等

C．顶角相等的两个等腰三角形一定全等

D．底边相等的两个等腰直角三角形一定全等

如图，在△ABC中，已知∠ABC=46°，∠ACB=80°，延长BC至D，使CD=CA，连接AD，则∠BAD的度数

A．

B．

C．

D．

如图AB＝AC，∠AEB＝∠ADC＝90°，则判断△ABE≌△ACD的方法是

A．AAS

B．HL

C．SSS

D．SAS

如图所示，≌，若，则为

A．

B．

C．

D．

如图（1），Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D。AF平分∠CAB，交CD于点E，交CB于点F。

（1）求证：CE=CF。
（2）将图（1）中的△ADE沿AB向右平移到△A′D′E′的位置，使点E′落在BC边上，其它条件不变，如图(2)所示。试猜想：BE′与CF有怎样的数量关系？请证明你的结论。

如图，在△ADF与△CBE中，点A 、E、F、C在同一直线上，已知AD∥BC，AD=CB，AE=CF．求证：DF=BE．