如图，△ABC中BD、CD平分∠ABC、∠ACB，过D作直线平行于BC，交AB、AC于E、F，当∠A的位置及大小变化时，线段EF和BE+CF的大小关系是（ ）
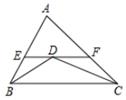
A．EF=BE+CF B．EF＞BE+CF C．EF＜BE+CF D．不能确定
如图所示，△ABC≌△AEF，有以下结论：①AC=AF；②∠C=∠E；③EF=BC；④∠EAB=∠FAC，其中正确的个数是（ ）
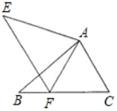
| A．1个 | B．2个 | C．3个 | D．4个 |
如图，下列条件中，不能证明
的是（ ）
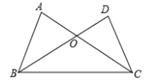
| A．AB=DC，AC=DB |
| B．AC=DB，∠ACB=∠DBC |
| C．AB=DC，∠ACB=∠DBC |
| D．BO=CO，∠A=∠D |
如图，工人师傅砌门时，常用木条EF固定长方形门框ABCD，使其不变形，这样做的根据是（ ）
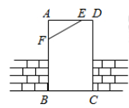
| A．两点之间线段最短 | B．两点确定一条直线 |
| C．长方形是轴对称图形 | D．三角形具有稳定性 |
阅读课本材料，解答后面的问题．
折纸与证明
折纸，常常能为证明一个命题提供思路和方法．例如，在△ABC中，AB＞AC（图27－1），怎样证明∠C＞
∠B呢？
把AC沿∠A的平分线AD翻折，因为AB＞AC，所以，点C落在AB上的点C’处（图27－2）．于是，由∠AC’D＞∠B，可得∠C＞∠B．
在△ABC中，∠B=2∠C，点D为线段BC上一动点，当AD满足某种条件时，探讨在线段AB、BD、CD、AC四条线段中，某两条或某三条线段之间存在的数量关系．
（1）如图3，当AD⊥BC时，求证：AB+BD=DC；
（2）如图4，当AD是∠BAC的角平分线时，写出AB、BD、AC的数量关系，并证明．
如图：E在△ABC的AC边的延长线上，D点在AB边上，DE交BC于点F， DF=EF，BD=CE，过D作DG∥AC交BC于G．
求证：（1）△GDF≌△CEF；
（2）若AB＝5，BC＝6，求△ABC的面积．
如图，四边形ABCD的对角线AC与BD相交于点O，∠1＝∠2，∠3＝∠4．
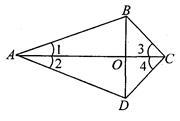
求证：（1） BC＝DC； （2） AC⊥BD．
如图，△ABC中，
，
，AB＝AC．
（1）求
的度数；
（2）求证：BC=BD=AD．
如图，一次“台风”过后，一根旗杆被台风从离地面2．8米处吹断裂，倒下的旗杆的顶端落在离旗杆底部9．6米处，那么这根旗杆被吹断裂前有多高?（旗杆粗细、断裂磨损忽略不计）
如图，在△ABC中，CD是AB边的中线，∠CDB＝60°，将△BCD沿CD折叠，使点B落在点E的位置．证明：△ADE是等边三角形．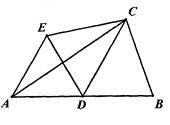
如图，已知：在△AFD和△CEB中，点A、E、F、C在同一直线上，AE=CF， AD=BC，AD∥BC．求证：DF∥BE．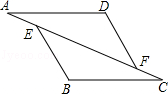
试题篮
()
粤公网安备 44130202000953号
的取值范围是（ ）
的度数是（ ）
，则它的顶角为（ ）
