如图11,AD是△ABC的角平分线,DE、DF分别是△ABD和△AC D的高,求证:AD垂直平分EF。(5分)
D的高,求证:AD垂直平分EF。(5分)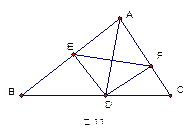
某厂房屋顶呈人字架形(等腰三角形),如图8所示,已知 m,
m, ,
, 于点
于点

(1)求 的大小.
的大小.
(2)求 的长度.
的长度.
如图①,P是△ABC边AC上的动点,以P为顶点作矩形PDEF,顶点D,E在边BC上,顶点F在边AB上;△ABC的底边BC及BC上的高的长分别为a , h,且是关于x的一元二次方程 的两个实数根,设过D, E,F三点的⊙O的面积为
的两个实数根,设过D, E,F三点的⊙O的面积为 ,矩形PDEF的面积为
,矩形PDEF的面积为

(1)求证:以a+h为边长的正方形面积与以a、h为边长的矩形面积之比不小于4;
(2)求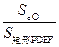 的最小值;
的最小值;
(3)当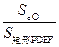 的值最小时,过点A作BC的平行线交直线BP与Q,这时线段AQ的长与m , n , k的取值是否有关?请说明理由。
的值最小时,过点A作BC的平行线交直线BP与Q,这时线段AQ的长与m , n , k的取值是否有关?请说明理由。
(本小题满分7分)如图,△ABC中,AB=AC,BD⊥AC,CE⊥AB.
求证:BD=CE.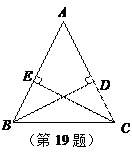
如图6,在正方形 中, 是 上的任意一点,( 与 、 两点不重合), 、 是 上的两点( 、 与 、 两点不重合),若 , ,请判断线段 与 有怎样的位置关系,并证明你的结论.

(6分)如图,点B、D、C、F在一条直线上,且BC = FD,AB = EF.
(1)请你只添加一个条件(不再加辅助线),使△ABC≌△EFD,你添加的条件是 ;
(2)添加了条件后,证明△ABC≌△EFD.
如图,在⊙O中,直径AB垂直于弦CD,垂足为E,连接AC,
将△ACE沿AC翻折得到△ACF,直线FC与直线AB相交于点G.
(1)直线FC与⊙O有何位置关系?并说明理由;
(2)若 ,求CD的长.
,求CD的长.
如图,点B和点C分别为∠MAN两边上的点,AB=AC.
(1)按下列语句画出图形:
① AD⊥BC,垂足为D;
② ∠BCN的平分线CE与AD的延长线交于点E
③ 连结BE.
(2)在完成(1)后不添加线段和字母的情况下,请你写出除△ABD≌△ACD外的两对全等三角形: ≌ , ≌ ;并选择其中的一对全等三角形予以证明.
(满分8分)如图9,在正方形网格中,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
(1)将△ABC向右平移5个单位长度,画出平移后的△A1B1C1 ;
(2)画出△ABC关于x轴对称的△A2B2C2 ;
(3)将△ABC绕原点O 旋转180°,画出旋转后的△A3B3C3 ;
(4)在△A1B1C1 、△A2B2C2 、△A3B3C3 中△________与△________成轴对称;△________与△________成中心对称.
(本题满分10分)如图,圆O的直径为5,在圆O上位于直径AB的异侧有定点C和动点P,已知BC∶CA=4∶3,点P在半圆弧AB上运动(不与A、B重合),过C作CP的垂线CD交PB的延长线于D点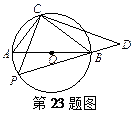
(1)求证:AC·CD=PC·BC;
(2)当点P运动到AB弧中点时,求CD的长;
(3)当点P运动到什么位置时,△PCD的面积最大?并求这个最大面积S.
(本题满分9分)将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展平纸片,如图(1);再次折叠该三角形纸片,使得点A与点D重合,折痕为EF,再次展平后连接DE、DF,如图2,证明:四边形AEDF是菱形.
如图1,在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若B、P在直线a的异侧, BM^直线a于点M,CN^直线a于点N,连接PM、PN;
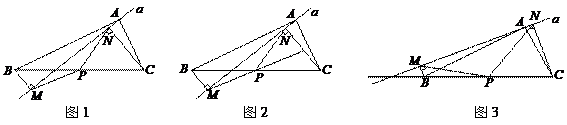 (1) 延长MP交CN于点E(如图2)。j求证:△BPM@△CPE;k求证:PM = PN;
(1) 延长MP交CN于点E(如图2)。j求证:△BPM@△CPE;k求证:PM = PN;
(2) 若直线a绕点A旋转到图3的位置时,点B、P在直线a的同侧,其它条件不变。此时PM=PN还成立吗?若成立,请给予证明;若不成立,请说明理由;
(3) 若直线a绕点A旋转到与BC边平行的位置时,其它条件不变。请直接判断四边形MBCN
的形状及此时PM=PN还成立吗?不必说明理由。
如图,△ABC内接于⊙O,AD⊥BC,OE⊥BC, OE= BC.
BC.
(1)求∠BAC的度数.
(2)将△ACD沿AC折叠为△ACF,将△ABD沿AB折叠为△ABG,延长FC和GB相交于点H.求证:四边形AFHG是正方形.
(3)若BD=6,CD=4,求AD的长.
如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.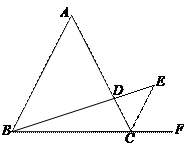
(1)求证:△ABD∽△CED.
(2)若AB=6,AD=2CD,求BE的长.
试题篮
()