初中数学圆幂定理解答题

如图①、②，在平面直角坐标系中，点A的坐标为（4，0），以点A为圆心，4为半径的圆与轴于O，B两点，OC为弦，∠AOC=60°，P是轴上的一动点，连结CP．

（1）求的度数；
（2）如图①，当与⊙A相切时，求的长；
（3）如图②，当点在直径上时，的延长线与⊙A相交于点，问为何值时，是等腰三角形？

（1）引入：如图1，直线AB为⊙O的弦，OC⊥OA,交AB于点P,且PC=BC，直线BC是否与⊙O相切，为什么？

（2）引申：记（1）中⊙O的切线为直线，在（1）的条件下，如图2，将切线向下平移，设平移后的直线与OB的延长线相交于点，与AB的延长线相交于点E，与OP的延长线相交于点．
找出图2中与相等的线段，并说明理由；
如果=9cm，=12cm，⊙O的半径为6cm，试求线段的长．

如图，⊙O的半径OD⊥弦AB于点C，连结AO并延长交⊙O于点E，连结EC．已知AB＝8，CD＝2．

（1）求⊙O的半径； 
（2）求sin∠BCE的值．

如图，以矩形ABCD的对角线AC的中点O为圆心、OA长为半径作⊙O，⊙O经过B、D两点，过点B作BK⊥AC，垂足为K，过点D作DH∥KB，DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H。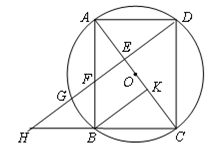

（1）求证：AE＝CK
（2）若AB＝a，AD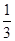＝a（a为常数），求BK的长（用含a的代数式表示）。
（3）若F是EG的中点，且DE＝6，求⊙O的半径和GH的长。

如图，点在的直径的延长线上，点在上，，

（1）求证：CD是的切线；
（2）若的半径为3，求CD的长．

．如图，BE是⊙O的直径，点A在EB的延长线上，弦PD⊥BE，垂足为C，连接OD，∠AOD=∠APC．

（1）求证：AP是⊙O的切线．
（2）若⊙O的半径是4，AP=4，求图中阴影部分的面积．

如图，在平面直角坐标系中，一段圆弧经过格点A、B、C．

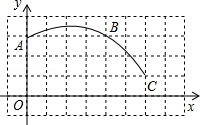
（1）请写出该圆弧所在圆的圆心O的坐标    ；
（2）⊙O的半径为         （结果保留根号）；
（3）求的长（结果保留π）．

如图，已知AB是⊙O的直径，P为⊙O外一点，且OP∥BC，∠P=∠BAC．

（1）求证：PA为⊙O的切线；
（2）若OB=5，OP=，求AC的长．

如图，在直角坐标系中，已知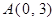、、、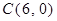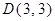，点P从C点出发，沿着折线C﹣D﹣A运动到达点A时停止，过C点作直线GC⊥PC，且与过O、P、C三点的⊙M交于点G，连接OP、PG、OD．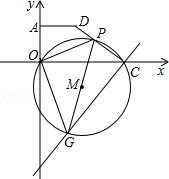

（1）直接写出∠DCO的度数；
（2）当点P在线段CD上运动时，求△OPG的最小面积；
（3）设圆心M的纵坐标为n，试探索：在点P运动的整个过程中，n的取值范围．

如图所示，已知圆锥底面半径r=10cm，母线长为40cm．

（1）求它的侧面展开图的圆心角；
（2）若一甲虫从A点出发沿着圆锥侧面行到母线SA的中点B，求它所走的最短路线。

如图，在平面直角坐标系中，⊙A与x轴相交于C（﹣2，0），D（﹣8，0）两点，与y轴相切于点B（0，4）．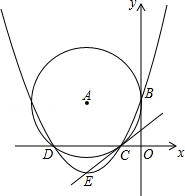

（1）求经过B，C，D三点的抛物线的函数表达式；
（2）设抛物线的顶点为E，证明：直线CE与⊙A相切；
（3）在x轴下方的抛物线上，是否存在一点F，使△BDF面积最大，最大值是多少？并求出点F的坐标．

如图，矩形OACB，A（0，3）、B（6，0），点E在线段OB上，∠AEO=30°，点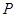从点Q（-4，0）出发，沿x轴向右以每秒1个单位长度的速度运动，运动时间为t秒．

（1）求点E的坐标；
（2）当∠PAE=15°时，求t的值；
（3）以点P为圆心，PA为半径的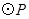随点P的运动而变化，当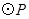与四边形AEBC的边（或边所在的直线）相切时，求t的值．

如图，半圆O的直径DE＝12cm，Rt△ABC中，∠ACB＝90°，∠ABC＝30°，BC＝12cm．半圆O以2cm/s的速度从左向右运动，在运动过程中，直径DE始终在直线BC上．设运动时间为t（s），当t＝0（s）时，半圆O在△ABC的左侧，OC＝8cm．

（1）外
当t＝8（s）时，试判断点C与半圆O所在的圆的位置关系．
外
（2）当t为何值时，△ABC的一边所在直线与半圆O所在的圆相切．
（3）在（2）的条件下，如果半圆O与△ABC三边围成的区域有重叠部分，求重叠部分的面积．

如图，⊙O的半径为1，直线CD经过圆心O，交⊙O于C、D两点，直径AB⊥CD，点M是直线CD上异于点C、O、D的一个动点，AM所在的直线交于⊙O于点N，点P是直线CD上另一点，且PM=PN．

（1）当点M在⊙O内部，如图一，试判断PN与⊙O的关系，并写出证明过程；
（2）当点M在⊙O外部，如图二，其它条件不变时，（1）的结论是否成立？请说明理由；
（3）当点M在⊙O外部，如图三，∠AMO=30°，求图中阴影部分的面积．

如图，已知等边△ABC，AB=16，以AB为直径的半圆与BC边交于点D，过点D作DF⊥AC，垂足为F，过点F作FG⊥AB，垂足为G，连结GD．

（1）求证：DF是⊙O的切线；
（2）求FG的长；
（3）求tan∠FGD的值．