初中数学计算题

先化简，再求值： $(\frac{1}{x+3}-\frac{1}{3-x})÷\frac{2}{x-3}$ ，其中， $x=\sqrt{3}-3$ ．

解不等式组： $\left\{\begin{array}{c}x-3(x-1)⩾5\\ \frac{x-3}{5}-1<\frac{x+1}{2}\end{array}\right.$

在边长为2的等边三角形 $\mathit{ABC}$ 中， $P$ 是 $\mathit{BC}$ 边上任意一点，过点 $P$ 分别作 $\mathit{PM}\perp \mathit{AB}$ ， $\mathit{PN}\perp \mathit{AC}$ ， $M$ 、 $N$ 分别为垂足．

（1）求证：不论点 $P$ 在 $\mathit{BC}$ 边的何处时都有 $\mathit{PM}+\mathit{PN}$ 的长恰好等于三角形 $\mathit{ABC}$ 一边上的高；

（2）当 $\mathit{BP}$ 的长为何值时，四边形 $\mathit{AMPN}$ 的面积最大，并求出最大值．

为确保广大居民家庭基本用水需求的同时鼓励家庭节约用水，对居民家庭每户每月用水量采用分档递增收费的方式，每户每月用水量不超过基本用水量的部分享受基本价格，超出基本用水量的部分实行超价收费．为对基本用水量进行决策，随机抽查2000户居民家庭每户每月用水量的数据，整理绘制出下面的统计表：

用户每月用水量 $\left(m^3\right)$	32及其以下	33	34	35	36	37	38	39	40	41	42	43及其以上
户数（户）	200	160	180	220	240	210	190	100	170	120	100	110

（1）为确保 $70\%$ 的居民家庭每户每月的基本用水量需求，那么每户每月的基本用水量最低应确定为多少立方米？

（2）若将（1）中确定的基本用水量及其以内的部分按每立方米1.8元交费，超过基本用水量的部分按每立方米2.5元交费．设 $x$ 表示每户每月用水量（单位： $m^3$ ）， $y$ 表示每户每月应交水费（单位：元），求 $y$ 与 $x$ 的函数关系式；

（3）某户家庭每月交水费是80.9元，请按以上收费方式计算该家庭当月用水量是多少立方米？

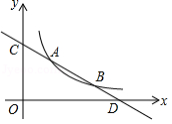
直线 $y=\mathit{kx}+b$ 与反比例函数 $y=\frac{6}{x}(x>0)$ 的图象分别交于点 $A(m,3)$ 和点 $B(6,n)$ ，与坐标轴分别交于点 $C$ 和点 $D$ ．

（1）求直线 $\mathit{AB}$ 的解析式；

（2）若点 $P$ 是 $x$ 轴上一动点，当 $\mathit{\Delta COD}$ 与 $\mathit{\Delta ADP}$ 相似时，求点 $P$ 的坐标．

某商店分两次购进 $A$ 、 $B$ 两种商品进行销售，两次购进同一种商品的进价相同，具体情况如下表所示：

	购进数量（件）		购进所需费用（元）
	$A$	$B$
第一次	30	40	3800
第二次	40	30	3200

（1）求 $A$ 、 $B$ 两种商品每件的进价分别是多少元？

（2）商场决定 $A$ 种商品以每件30元出售， $B$ 种商品以每件100元出售．为满足市场需求，需购进 $A$ 、 $B$ 两种商品共1000件，且 $A$ 种商品的数量不少于 $B$ 种商品数量的4倍，请你求出获利最大的进货方案，并确定最大利润．

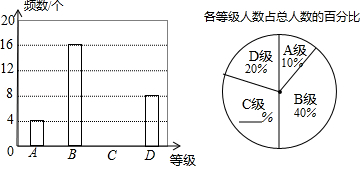
校园广播主持人培训班开展比赛活动，分为 $A$ 、 $B$ 、 $C$ 、 $D$ 四个等级，对应的成绩分别是9分、8分、7分、6分，根据如图不完整的统计图解答下列问题：

（1）补全下面两个统计图（不写过程）；

（2）求该班学生比赛的平均成绩；

（3）现准备从等级 $A$ 的4人（两男两女）中随机抽取两名主持人，请利用列表或画树状图的方法，求恰好抽到一男一女学生的概率？

解方程： $\frac{x+3}{x-3}-\frac{4}{x+3}=1$ ．

解不等式组： $\left\{\begin{array}{c}3x+6⩾5(x-2)\\ \frac{x-5}{2}-\frac{4x-3}{3}<1\end{array}\right.$．

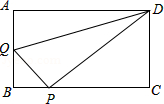
在矩形 $\mathit{ABCD}$ 中， $\mathit{AB}=3$ ， $\mathit{AD}=4$ ，动点 $Q$ 从点 $A$ 出发，以每秒1个单位的速度，沿 $\mathit{AB}$ 向点 $B$ 移动；同时点 $P$ 从点 $B$ 出发，仍以每秒1个单位的速度，沿 $\mathit{BC}$ 向点 $C$ 移动，连接 $\mathit{QP}$ ， $\mathit{QD}$ ， $\mathit{PD}$ ．若两个点同时运动的时间为 $x$ 秒 $(0<x⩽3)$ ，解答下列问题：

（1）设 $\mathit{\Delta QPD}$ 的面积为 $S$ ，用含 $x$ 的函数关系式表示 $S$ ；当 $x$ 为何值时， $S$ 有最大值？并求出最小值；

（2）是否存在 $x$ 的值，使得 $\mathit{QP}\perp \mathit{DP}$ ？试说明理由．

某种水彩笔，在购买时，若同时额外购买笔芯，每个优惠价为3元，使用期间，若备用笔芯不足时需另外购买，每个5元．现要对在购买水彩笔时应同时购买几个笔芯作出选择，为此收集了这种水彩笔在使用期内需要更换笔芯个数的30组数据，整理绘制出下面的条形统计图：

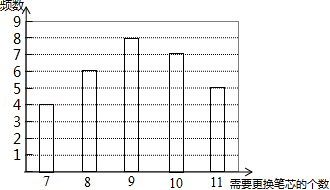
设 $x$ 表示水彩笔在使用期内需要更换的笔芯个数， $y$ 表示每支水彩笔在购买笔芯上所需要的费用（单位：元）， $n$ 表示购买水彩笔的同时购买的笔芯个数．

（1）若 $n=9$ ，求 $y$ 与 $x$ 的函数关系式；

（2）若要使这30支水彩笔"更换笔芯的个数不大于同时购买笔芯的个数"的频率不小于0.5，确定 $n$ 的最小值；

（3）假设这30支笔在购买时，每支笔同时购买9个笔芯，或每支笔同时购买10个笔芯，分别计算这30支笔在购买笔芯所需费用的平均数，以费用最省作为选择依据，判断购买一支水彩笔的同时应购买9个还是10个笔芯．

如图， $\text{Rt}\Delta \text{ABO}$ 的顶点 $O$ 在坐标原点，点 $B$ 在 $x$ 轴上， $\angle \mathit{ABO}=90°$ ， $\angle \mathit{AOB}=30°$ ， $\mathit{OB}=2\sqrt{3}$ ，反比例函数 $y=\frac{k}{x}(x>0)$ 的图象经过 $\mathit{OA}$ 的中点 $C$ ，交 $\mathit{AB}$ 于点 $D$ ．

（1）求反比例函数的关系式；

（2）连接 $\mathit{CD}$ ，求四边形 $\mathit{CDBO}$ 的面积．

某种型号油电混合动力汽车，从 $A$ 地到 $B$ 地燃油行驶纯燃油费用76元，从 $A$ 地到 $B$ 地用电行驶纯电费用26元，已知每行驶1千米，纯燃油费用比纯用电费用多0.5元．

（1）求每行驶1千米纯用电的费用；

（2）若要使从 $A$ 地到 $B$ 地油电混合行驶所需的油、电费用合计不超过39元，则至少用电行驶多少千米？

在等边 $\mathit{\Delta ABC}$ 中，点 $D$ ， $E$ 分别在边 $\mathit{BC}$ 、 $\mathit{AC}$ 上，若 $\mathit{CD}=2$ ，过点 $D$ 作 $\mathit{DE}//\mathit{AB}$ ，过点 $E$ 作 $\mathit{EF}\perp \mathit{DE}$ ，交 $\mathit{BC}$ 的延长线于点 $F$ ，求 $\mathit{EF}$ 的长．

为了解学生的体能情况，随机选取了1000名学生进行调查，并记录了他们对长跑、短跑、跳绳、跳远四个项目的喜欢情况，整理成以下统计表，其中" $\surd$ "表示喜欢，" $\times$ "表示不喜欢．

	长跑	短跑	跳绳	跳远
200	$\surd$	$\times$	$\surd$	$\surd$
300	$\times$	$\surd$	$\times$	$\surd$
150	$\surd$	$\surd$	$\surd$	$\times$
200	$\surd$	$\times$	$\surd$	$\times$
150	$\surd$	$\times$	$\times$	$\times$

（1）估计学生同时喜欢短跑和跳绳的概率；

（2）估计学生在长跑、短跑、跳绳、跳远中同时喜欢三个项目的概率；

（3）如果学生喜欢长跑、则该同学同时喜欢短跑、跳绳、跳远中哪项的可能性大？