如图,已知 的三个顶点 、 、 , ,作 关于直线 的对称图形
(1)若 ,试求四边形 面积 的最大值;
(2)若点 恰好落在 轴上,试求 的值.
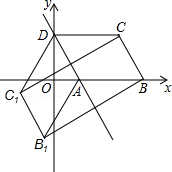
已知二次函数 的图象与 轴的负半轴和正半轴分别交于 、 两点,与 轴交于点 ,它的顶点为 ,直线 与过点 且垂直于 轴的直线交于点 ,且
(1)求 、 两点的坐标;
(2)若 ,求这个二次函数的关系式.
某公司今年如果用原线下销售方式销售一产品,每月的销售额可达100万元.由于该产品供不应求,公司计划于3月份开始全部改为线上销售,这样,预计今年每月的销售额 (万元)与月份 (月)之间的函数关系的图象如图1中的点状图所示(5月及以后每月的销售额都相同),而经销成本 (万元)与销售额 (万元)之间函数关系的图象图2中线段 所示.

(1)求经销成本 (万元)与销售额 (万元)之间的函数关系式;
(2)分别求该公司3月,4月的利润;
(3)问:把3月作为第一个月开始往后算,最早到第几个月止,该公司改用线上销售后所获得利润总额比同期用线下方式销售所能获得的利润总额至少多出200万元?(利润 销售额 经销成本)
甲、乙两队进行打乒乓球团体赛,比赛规则规定:两队之间进行3局比赛,3局比赛必须全部打完,只要赢满2局的队为获胜队,假如甲、乙两队之间每局比赛输赢的机会相同,且甲队已经赢得了第1局比赛,那么甲队最终获胜的概率是多少?(请用“画树状图”或“列表”等方法写出分析过程)
已知两个二次函数 和 .对于函数 ,当 时,该函数取最小值.
(1)求 的值;
(2)若函数 的图象与坐标轴只有2个不同的公共点,求这两个公共点间的距离;
(3)若函数 、 的图象都经过点 ,过点 , 为实数)作 轴的平行线,与函数 、 的图象共有4个不同的交点,这4个交点的横坐标分别是 、 、 、 ,且 ,求 的最大值.
如图,点 , 在反比例函数 的图象上,经过点 、 的直线与 轴相交于点 ,与 轴相交于点 .
(1)若 ,求 的值;
(2)求 的值;
(3)连接 、 ,若 ,求直线 的函数关系式.

如图,地面上两个村庄 、 处于同一水平线上,一飞行器在空中以6千米 小时的速度沿 方向水平飞行,航线 与 、 在同一铅直平面内.当该飞行器飞行至村庄 的正上方 处时,测得 ;该飞行器从 处飞行40分钟至 处时,测得 .求村庄 、 间的距离 取1.73,结果精确到0.1千米)

随着互联网的迅速发展,某购物网站的年销售额从2013年的200万元增长到2015年的392万元.求该购物网站平均每年销售额增长的百分率.
如图,在平面直角坐标系 中,将二次函数 的图象 沿 轴翻折,把所得到的图象向右平移2个单位长度后再向上平移8个单位长度,得到二次函数图象 .
(1)求 的函数表达式;
(2)设点 是以点 为圆心、1为半径的圆上一动点,二次函数的图象 与 轴相交于两点 、 ,求 的最大值;
(3)若一个点的横坐标与纵坐标均为整数,则该点称为整点.求 与 所围成封闭图形内(包括边界)整点的个数.

已知 是等腰直角三角形, , 是边 上一动点 、 两点除外),将 绕点 按逆时针方向旋转角 得到 ,其中点 是点 的对应点,点 是点 的对应点.

(1)如图1,当 时, 是边 上一点,且 ,连接 .求证: ;
(2)如图2,当 时, 与 相交于点 .
①当点 与点 、 不重合时,连接 ,求 的度数;
②设 为边 的中点,当 从 变化到 时,求点 运动的路径长.
某景点试开放期间,团队收费方案如下:不超过30人时,人均收费120元;超过30人且不超过 人时,每增加1人,人均收费降低1元;超过 人时,人均收费都按照 人时的标准.设景点接待有 名游客的某团队,收取总费用为 元.
(1)求 关于 的函数表达式;
(2)景点工作人员发现:当接待某团队人数超过一定数量时,会出现随着人数的增加收取的总费用反而减少这一现象.为了让收取的总费用随着团队中人数的增加而增加,求 的取值范围.
试题篮
()