如图, 是 内一点, 与 相交于 、 两点,且与 、 分别相切于点 、 , ,连接 、 .
(1)求证: .
(2)已知 , ,求四边形 是矩形时 的半径.
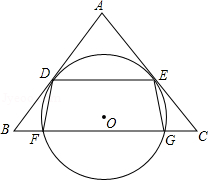
图中是抛物线拱桥, 处有一照明灯,水面 宽 ,从 、 两处观测 处,仰角分别为 、 ,且 , ,以 为原点, 所在直线为 轴建立直角坐标系.
(1)求点 的坐标;
(2)水面上升 ,水面宽多少 取1.41,结果精确到 ?

如图中的折线 表示某汽车的耗油量 (单位: 与速度 (单位: 之间的函数关系 ,已知线段 表示的函数关系中,该汽车的速度每增加 ,耗油量增加 .
(1)当速度为 、 时,该汽车的耗油量分别为 、 .
(2)求线段 所表示的 与 之间的函数表达式.
(3)速度是多少时,该汽车的耗油量最低?最低是多少?

如图,在平面直角坐标系 中,抛物线 经过两点 , .过点 作 轴,交抛物线于点 ,交 轴于点 .
(1)求此抛物线对应的函数表达式及点 的坐标;
(2)若抛物线上存在点 ,使得 的面积为 ,求出点 的坐标;
(3)连接 、 、 、 ,在坐标平面内,求使得 与 相似(边 与边 对应)的点 的坐标.

如图,在 中, , , .
(1)求 的长;
(2)利用此图形求 的值(精确到0.1,参考数据: , ,

环保局对某企业排污情况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的 .环保局要求该企业立即整改,在15天以内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度 与时间 (天 的变化规律如图所示,其中线段 表示前3天的变化规律,从第3天起,所排污水中硫化物的浓度 与时间 成反比例关系.
(1)求整改过程中硫化物的浓度 与时间 的函数表达式;
(2)该企业所排污水中硫化物的浓度,能否在15天以内不超过最高允许的 ?为什么?

某数学兴趣小组研究我国古代《算法统宗》里这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.
(1)求该店有客房多少间?房客多少人?
(2)假设店主李三公将客房进行改造后,房间数大大增加.每间客房收费20钱,且每间客房最多入住4人,一次性订客房18间以上(含18间),房费按8折优惠.若诗中“众客”再次一起入住,他们如何订房更合算?
问题背景:
如图①,在四边形 中, , ,探究线段 , , 之间的数量关系.
小吴同学探究此问题的思路是:将 绕点 ,逆时针旋转 到 处,点 , 分别落在点 , 处(如图② ,易证点 , , 在同一条直线上,并且 是等腰直角三角形,所以 ,从而得出结论: .
简单应用:
(1)在图①中,若 , ,则 .
(2)如图③, 是 的直径,点 、 在 上, ,若 , ,求 的长.
拓展规律:
(3)如图④, , ,若 , ,求 的长(用含 , 的代数式表示)
(4)如图⑤, , ,点 为 的中点,若点 满足 , ,点 为 的中点,则线段 与 的数量关系是 .
如图,在平面直角坐标系中,二次函数 的图象与坐标轴交于 、 、 三点,其中点 的坐标为 ,点 的坐标为 .
(1)求该二次函数的表达式及点 的坐标;
(2)点 的坐标为 ,点 为该二次函数在第一象限内图象上的动点,连接 、 ,以 、 为邻边作平行四边形 ,设平行四边形 的面积为 .
①求 的最大值;
②在点 的运动过程中,当点 落在该二次函数图象上时,请直接写出此时 的值.

甲、乙两家草莓采摘园的草莓品质相同,销售价格也相同.“五一期间”,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园需购买60元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,设某游客的草莓采摘量为 (千克),在甲采摘园所需总费用为 (元 ,在乙采摘园所需总费用为 (元 ,图中折线 表示 与 之间的函数关系.
(1)甲、乙两采摘园优惠前的草莓销售价格是每千克 元;
(2)求 、 与 的函数表达式;
(3)在图中画出 与 的函数图象,并写出选择甲采摘园所需总费用较少时,草莓采摘量 的范围.

试题篮
()