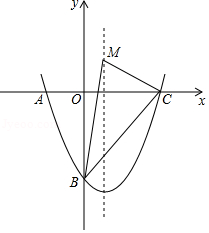
如图,抛物线 经过点 , ,并与 轴交于点 ,点 是抛物线对称轴 上任意一点(点 , , 三点不在同一直线上).
(1)求该抛物线所表示的二次函数的表达式;
(2)在抛物线上找出两点 , ,使得△ 与 全等,并求出点 , 的坐标;
(3)在对称轴上是否存在点 ,使得 为直角,若存在,作出点 (用尺规作图,保留作图痕迹),并求出点 的坐标.
如图,已知直角坐标系中, 、 、 三点的坐标分别为 , , ,点 与点 关于 轴对称,连接 、 .
(1)求过 、 、 三点的抛物线的解析式;
(2)有一动点 从原点 出发,以每秒2个单位的速度向右运动,过点 作 轴的垂线,交抛物线于点 ,交线段 于点 ,连接 、 ,设点 运动的时间为 秒,求四边形 的面积 与 的函数关系式,并求出四边形 的最大面积;
(3)抛物线的对称轴上是否存在一点 ,使得 是直角三角形?若存在,请直接写出点 的坐标;若不存在,请说明理由.

如图, 的圆心 , 经过坐标原点 ,与 轴交于点 .经过点 的一条直线 解析式为: 与 轴交于点 ,以 为顶点的抛物线经过 轴上点 和点 .
(1)求抛物线的解析式;
(2)求证:直线 是 的切线;
(3)点 为抛物线上一动点,且 与直线 垂直,垂足为 ; 轴,交直线 于点 ,是否存在这样的点 ,使 的面积最小.若存在,请求出此时点 的坐标及 面积的最小值;若不存在,请说明理由.

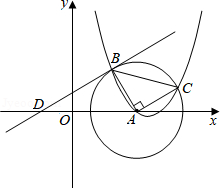
如图,已知 的圆心为点 ,抛物线 过点 ,与 交于 、 两点,连接 、 ,且 , 、 两点的纵坐标分别是2、1.
(1)请直接写出点 的坐标,并求 、 的值;
(2)直线 经过点 ,与 轴交于点 .点 (与点 不重合)在该直线上,且 ,请判断点 是否在此抛物线上,并说明理由;
(3)如果直线 与 相切,请直接写出满足此条件的直线解析式.
如图,一次函数 的图象与坐标轴交于 , 两点,与反比例函数 的图象交于 , 两点,过点 作 轴于点 ,已知 .
(1)求 的值;
(2)若 ,求反比例函数的解析式;
(3)在(2)的条件下,设点 是 轴(除原点 外)上一点,将线段 绕点 按顺时针或逆时针旋转 得到线段 ,当点 滑动时,点 能否在反比例函数的图象上?如果能,求出所有的点 的坐标;如果不能,请说明理由.

我们知道,经过原点的抛物线可以用 表示,对于这样的抛物线:
(1)当抛物线经过点 和 时,求抛物线的表达式;
(2)当抛物线的顶点在直线 上时,求 的值;
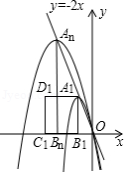
(3)如图,现有一组这样的抛物线,它们的顶点 、 、 , 在直线 上,横坐标依次为 , , , , 为正整数,且 ,分别过每个顶点作 轴的垂线,垂足记为 、 , , ,以线段 为边向左作正方形 ,如果这组抛物线中的某一条经过点 ,求此时满足条件的正方形 的边长.
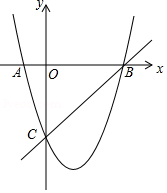
如图,在平面直角坐标系中,二次函数的图象交坐标轴于 , , 三点,点 是直线 下方抛物线上一动点.
(1)求这个二次函数的解析式;
(2)是否存在点 ,使 是以 为底边的等腰三角形?若存在,求出 点坐标;若不存在,请说明理由;
(3)动点 运动到什么位置时, 面积最大,求出此时 点坐标和 的最大面积.
如图甲,直线 与 轴、 轴分别交于点 、点 ,经过 、 两点的抛物线 与 轴的另一个交点为 ,顶点为 .
(1)求该抛物线的解析式;
(2)在该抛物线的对称轴上是否存在点 ,使以 , , 为顶点的三角形为等腰三角形?若存在,请直接写出所符合条件的点 的坐标;若不存在,请说明理由;
(3)当 时,在抛物线上求一点 ,使 的面积有最大值(图乙、丙供画图探究).

如图,在平面直角坐标系中, 的三个顶点分别是 , , , .抛物线 经过点 ,且对称轴为 ,并与 轴交于点 .
(1)求抛物线的解析式及点 的坐标;
(2)将 沿 轴向右平移 个单位,使 点移到点 ,然后将三角形绕点 顺时针旋转 得到 .若点 恰好落在抛物线上.
①求 的值;
②连接 交 轴于点 ,连接 ,过 作 ,交 于点 ,求证: .
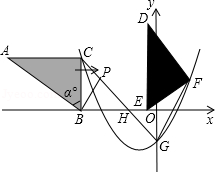
如图,在平面直角坐标系中, 的三个顶点分别是 , , , .抛物线 经过点 ,且对称轴为 ,并与 轴交于点 .
(1)求抛物线的解析式及点 的坐标;
(2)将 沿 轴向右平移 个单位,使 点移到点 ,然后将三角形绕点 顺时针旋转 得到 .若点 恰好落在抛物线上.
①求 的值;
②连接 交 轴于点 ,连接 ,过 作 ,交 于点 ,求证: .
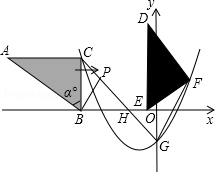
如图,抛物线 经过 , 两点,与 轴交于点 .
(1)求抛物线的解析式及顶点 的坐标;
(2)点 在抛物线的对称轴上,当 的周长最小时,求出点 的坐标;
(3)点 在抛物线上,点 在抛物线的对称轴上,是否存在以点 为直角顶点的 与 相似?若存在,请求出所有符合条件的点 的坐标;若不存在,请说明理由.

如图,二次函数 的图象与 轴的一个交点为 ,另一个交点为 ,且与 轴相交于 点.
(1)求 的值及 点坐标;
(2)在直线 上方的抛物线上是否存在一点 ,使得它与 , 两点构成的三角形面积最大,若存在,求出此时 点坐标;若不存在,请简要说明理由;
(3) 为抛物线上一点,它关于直线 的对称点为
①当四边形 为菱形时,求点 的坐标;
②点 的横坐标为 ,当 为何值时,四边形 的面积最大,请说明理由.

如图,四边形 是边长为4的正方形,点 为 边上任意一点(与点 、 不重合),连接 ,过点 作 交 于点 ,且 ,过点 作 ,交 于点 ,连接 、 ,设 .
(1)求点 的坐标(用含 的代数式表示);
(2)试判断线段 的长度是否随点 的位置的变化而改变?并说明理由.
(3)当 为何值时,四边形 的面积最小;
(4)在 轴正半轴上存在点 ,使得 是等腰三角形,请直接写出不少于4个符合条件的点 的坐标(用含 的式子表示).

如图,直线 与 轴、 轴分别相交于点 、 ,经过 、 两点的抛物线 与 轴的另一个交点为 ,顶点为 ,且对称轴为直线 .
(1)求该抛物线的解析式;
(2)连接 、 ,求 的面积;
(3)连接 ,在 轴上是否存在一点 ,使得以点 , , 为顶点的三角形与 相似?若存在,求出点 的坐标;若不存在,请说明理由.

试题篮
()