如图所示,抛物线 与 轴相交于 、 两点,与 轴相交于点 ,点 为抛物线的顶点.
(1)求点 及顶点 的坐标.
(2)若点 是第四象限内抛物线上的一个动点,连接 、 ,求 面积的最大值及此时点 的坐标.
(3)若点 是抛物线对称轴上的动点,点 是抛物线上的动点,是否存在以点 、 、 、 为顶点的四边形是平行四边形.若存在,求出点 的坐标;若不存在,试说明理由.
(4)直线 交 轴于点 ,若点 是线段 上的一个动点,是否存在以点 、 、 为顶点的三角形与 相似.若存在,求出点 的坐标;若不存在,请说明理由.

如图1,平面直角坐标系 中,等腰 的底边 在 轴上, ,顶点 在 的正半轴上, ,一动点 从 出发,以每秒1个单位的速度沿 向左运动,到达 的中点停止.另一动点 从点 出发,以相同的速度沿 向左运动,到达点 停止.已知点 、 同时出发,以 为边作正方形 ,使正方形 和 在 的同侧,设运动的时间为 秒 .
(1)当点 落在 边上时,求 的值;
(2)设正方形 与 重叠面积为 ,请问是否存在 值,使得 ?若存在,求出 值;若不存在,请说明理由;
(3)如图2,取 的中点 ,连结 ,当点 、 开始运动时,点 从点 出发,以每秒 个单位的速度沿 运动,到达点 停止运动.请问在点 的整个运动过程中,点 可能在正方形 内(含边界)吗?如果可能,求出点 在正方形 内(含边界)的时长;若不可能,请说明理由.
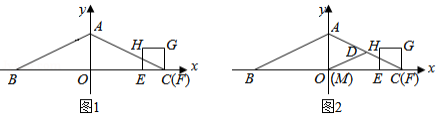
如图1,抛物线 与 轴交于 , ,与 轴交于点 .已知直线 过 , 两点.
(1)求抛物线和直线 的表达式;
(2)点 是抛物线上的一个动点.
①如图1,若点 在第一象限内,连接 ,交直线 于点 .设 的面积为 , 的面积为 ,求 的最大值;
②如图2,抛物线的对称轴 与 轴交于点 ,过点 作 ,垂足为 .点 是对称轴 上的一个动点,是否存在以点 , , , 为顶点的四边形是平行四边形?若存在,求出点 , 的坐标;若不存在,请说明理由.

已知 是 斜边 的中点, , ,过点 作 使 , ,连接 并延长 到 ,使 ,连接 , , ,设 与 交于 , 与 交于 .
(1)如图1,当 , , 共线时,求证:
① ;
② ;
(2)如图2,当 , , 不共线时,连接 ,求证: .
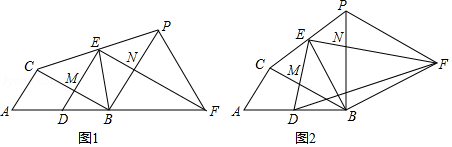
已知函数 , 均为一次函数, 为常数.

(1)如图1,将直线 绕点 逆时针旋转 得到直线 ,直线 交 轴于点 .若直线 恰好是 , 中某个函数的图象,请直接写出点 坐标以及 可能的值;
(2)若存在实数 ,使得 成立,求函数 , 图象间的距离;
(3)当 时,函数 图象分别交 轴, 轴于 , 两点, 图象交 轴于 点,将函数 的图象最低点 向上平移 个单位后刚好落在一次函数 图象上.设 的图象,线段 ,线段 围成的图形面积为 ,试利用初中知识,探究 的一个近似取值范围.(要求:说出一种得到 的更精确的近似值的探究办法,写出探究过程,得出探究结果,结果的取值范围两端的数值差不超过0.01.
在平面直角坐标系中,已知抛物线 与 轴交于 , 两点(点 在点 的左侧),与 轴交于点 ,顶点为点 .
(1)当 时,直接写出点 , , , 的坐标:
, , , ;
(2)如图1,直线 交 轴于点 ,若 ,求 的值和 的长;
(3)如图2,在(2)的条件下,若点 为 的中点,动点 在第三象限的抛物线上,过点 作 轴的垂线,垂足为 ,交 于点 ;过点 作 ,垂足为 .设点 的横坐标为 ,记 .
①用含 的代数式表示 ;
②设 ,求 的最大值.

如图,直线 交 轴于点 ,交 轴于点 ,抛物线 经过点 ,点 ,且交 轴于另一点 .
(1)直接写出点 ,点 ,点 的坐标及拋物线的解析式;
(2)在直线 上方的抛物线上有一点 ,求四边形 面积的最大值及此时点 的坐标;
(3)将线段 绕 轴上的动点 顺时针旋转 得到线段 ,若线段 与抛物线只有一个公共点,请结合函数图象,求 的取值范围.
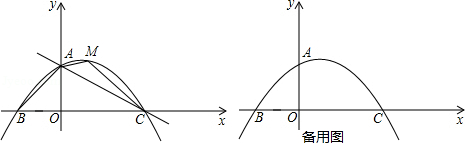
如图,在平面直角坐标系中,直线 与 轴交于点 ,与 轴交于点 ,抛物线 过点 且与直线相交于另一点 , .
(1)求抛物线的解析式;
(2)点 是抛物线上的一动点,当 时,求点 的坐标;
(3)点 , 在 轴的正半轴上,点 是 轴正半轴上的一动点,且满足 .
①求 与 之间的函数关系式;
②当 在什么范围时,符合条件的 点的个数有2个?

小华端午节从家里出发,沿笔直道路匀速步行去妈妈经营的商店帮忙,妈妈同时骑三轮车从商店出发,沿相同路线匀速回家装载货物,然后按原路原速返回商店,小华到达商店比妈妈返回商店早5分钟,在此过程中,设妈妈从商店出发开始所用时间为 (分钟),图1表示两人之间的距离 (米 与时间 (分钟)的函数关系的图象;图2中线段 表示小华和商店的距离 (米 与时间 (分钟)的函数关系的图象的一部分,请根据所给信息答案下列问题:
(1)填空:妈妈骑车的速度是 米 分钟,妈妈在家装载货物所用时间是 分钟,点 的坐标是 .
(2)直接写出妈妈和商店的距离 (米 与时间 (分钟)的函数关系式,并在图2中画出其函数图象;
(3)求 为何值时,两人相距360米.

将抛物线 向下平移6个单位长度得到抛物线 ,再将抛物线 向左平移2个单位长度得到抛物线 .
(1)直接写出抛物线 , 的解析式;
(2)如图(1),点 在抛物线 (对称轴 右侧)上,点 在对称轴 上, 是以 为斜边的等腰直角三角形,求点 的坐标;
(3)如图(2),直线 , 为常数)与抛物线 交于 , 两点, 为线段 的中点;直线 与抛物线 交于 , 两点, 为线段 的中点.求证:直线 经过一个定点.

如图,在平面直角坐标系中,抛物线 的对称轴为直线 ,其图象与 轴交于点 和点 ,与 轴交于点 .

(1)直接写出抛物线的解析式和 的度数;
(2)动点 , 同时从 点出发,点 以每秒3个单位的速度在线段 上运动,点 以每秒 个单位的速度在线段 上运动,当其中一个点到达终点时,另一个点也随之停止运动.设运动的时间为 秒,连接 ,再将线段 绕点 顺时针旋转 ,设点 落在点 的位置,若点 恰好落在抛物线上,求 的值及此时点 的坐标;
(3)在(2)的条件下,设 为抛物线上一动点, 为 轴上一动点,当以点 , , 为顶点的三角形与 相似时,请直接写出点 及其对应的点 的坐标.(每写出一组正确的结果得1分,至多得4分)
已知抛物线 过点 和 ,与 轴交于另一点 ,顶点为 .
(1)求抛物线的解析式,并写出 点的坐标;
(2)如图1, 为线段 上方的抛物线上一点, ,垂足为 , 轴,垂足为 ,交 于点 .当 时,求 的面积;
(3)如图2, 与 的延长线交于点 ,在 轴上方的抛物线上是否存在点 ,使 ?若存在,求出点 的坐标;若不存在,请说明理由.

如图1,在平面直角坐标系中, , ,以 为圆心, 的长为半径的半圆 交 延长线于 ,连接 , ,过 作 分别交 和半圆 于 , ,连接 , .
(1)求证: 是半圆 的切线;
(2)试判断四边形 的形状,并说明理由;
(3)如图2,若抛物线经过点 且顶点为 .
①求此抛物线的解析式;
②点 是此抛物线对称轴上的一个动点,以 , , 为顶点的三角形与 相似,问抛物线上是否存在一点 .使 ?若存在,请直接写出 点的横坐标;若不存在,说明理由.
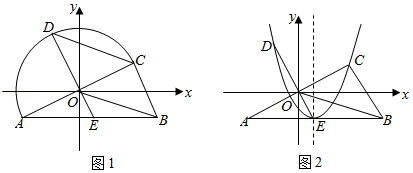
如图,抛物线 与 轴正半轴交于点 ,与 轴交于点 .
(1)求直线 的解析式及抛物线顶点坐标;
(2)如图1,点 为第四象限且在对称轴右侧抛物线上一动点,过点 作 轴,垂足为 , 交 于点 ,求 的最大值,并求出此时点 的坐标;
(3)如图2,将抛物线 向右平移得到抛物线 ,直线 与抛物线 交于 , 两点,若点 是线段 的中点,求抛物线 的解析式.

试题篮
()