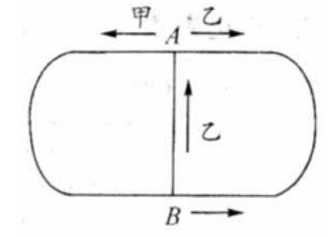
如图是一个长为 的环形跑道,其中 为跑道对称轴上的两点,且 之间有一条 的直线通道.甲乙两人同时从 点出发,甲按逆时针方向以速度 沿跑道跑步,当跑到 点时继续沿跑道前进,乙按顺时针方向以速度 沿跑道跑步,当跑到 点时沿直线通道跑回 点处,假设两人跑步的时间足够长.求:
(1)如果 ,那么甲跑了多少路程后,两人首次在 点处相遇;
(2)如果 ,那么乙跑了多少路程后,两人首次在 点处相遇.
某校九年级(1)班 名学生参加 跳绳体育考试. 跳绳次数与频数经统计后绘制出下面的频数分布表( 表示为大于等于 并且小于 )和扇形统计图,(如图).
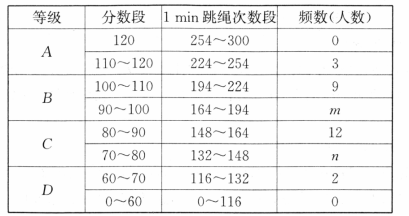
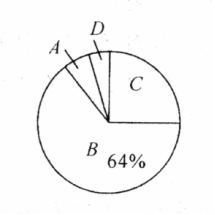
(1)求 的值;
(2)求该班 跳绳成绩在 分以上(含 分)的人数占全班人数的百分比;
(3)根据频数分布表估计该班学生 跳绳的平均分大约是多少?并说明理由.
为进一步建设秀美、宜居的生态环境,某村欲购买甲、乙、丙三种树美化村庄,已知甲、乙、丙三种树的价格之比为 ,丙种树每棵 元,现计划用 元资金,购买这三种树共 棵.
(1)求甲、乙两种树每棵各多少元?
(2)若购买甲种树的棵数是乙种树的 倍,恰好用完计划资金,则这三种树各能购买多少棵?
(3)若又增加了 元的购树款,在购买总棵数不变的前提下,求丙种树最多可购买多少棵?
探究:(1)如图①若 .则 .你能说明为什么吗?
(2)反之,若 ,直线 和 有什么位置关系,请证明;
(3)若将点 移至图②所示位置,此时 之间有什么关系?请证明;
(4)若将点 移至图③所示位置,情况又如何?
(5)在图④中, 与 又有何关系?
(6)在图⑤中,若 ,又得到什么结论?

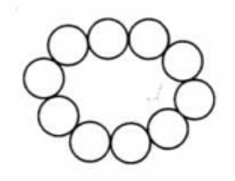
如图,将 这 个数字分别填入图中的 个圆圈内,使任意连续相邻的 个圆圈内的数字之和均不大于某一个整数 ,求 的最小值并完成相应的填图游戏.
甲、乙分别自 两地同时相向步行, 后在途中相遇,相遇后,甲、乙步行速度都提高了 ,当甲到达 地后立刻按原路向 地返回.当乙到达 地后也立刻按原路向 地返回.甲、乙二人在第一次相遇后 又再次相遇,则 两地的距离是多少?
江堤边发生管涌,江水不断涌到堤边一个原本干涸的池塘,假定每分钟涌出的水量相同,如果用两台抽水机抽水, 可以抽完池塘里的蓄水;如果用 台抽水机抽水, 可以抽完;如果要在 内将池塘里的蓄水抽完,那么至少需要抽水机多少台?
有一个四位数,把它从中间分成两半.得到前、后两个两位数,将前面的两位数的末尾添一个 ,然后加上前、后两个两位数的乘积,恰好等于原来的四位数,又知道原数的个位数字为 ,试求这个四位数.
用水平线和竖直线将平面分成若干个边长为 的小正方形格子,小正方形的顶点叫格点,以格点为顶点的多边形叫格点多边形.设格点多边形的面积为 ,它各边上格点的个数和为 .

(1)图①-④中的格点多边形,其内部都只有一个格点,它们的面积与各边上格点的个数和的对应关系如下表,请写出 与 之间的关系式.
答 _____.

(2)请你再画出一些格点多边形,使这些多边形内部都有而且只有 个格点.此时所画的各个多边形的面积 与它各边上格点的个数和 之间的关系是: _____.
(3)请你继续探索,当格点多边形内部有且只有 个格点时,猜想 与 有怎样的关系?
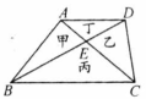
如图,三角形 内的线段 , 相交于点 ,已知 , .设 和四边形 的面积分别为 .
(1)求 的值;
(2)如果 ,求 的值.

如图,四边形 被 与 分成甲、乙、丙、丁 个三角形,已知 ,问:丙、丁两个三角形面积之和是甲、乙两个三角形面积之和的多少倍?
试题篮
()