如图,在等腰直角三角形 中,斜边
中,斜边 ,过点
,过点 作
作 的垂线,垂足为
的垂线,垂足为 ;过点
;过点 作
作 的垂线,垂足为
的垂线,垂足为 ;过点
;过点 作
作 的垂线,垂足为
的垂线,垂足为 ;…,以此类推,设
;…,以此类推,设 ,
, ,
, ,…,
,…, ,则
,则 ________.
________.
下列推理中属于类比推理的是( )
A.一切偶数都能被2整除,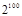 是偶数,所以 是偶数,所以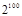 能被2整除. 能被2整除. |
B.由 …,归纳出数列的通项公式 …,归纳出数列的通项公式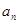 |
| C.由平面三角形的性质,推测空间四边形的性质 |
| D.如果a>b, c>d,则a-d>b-c |
面积为 的平面凸四边形的第
的平面凸四边形的第 条边的边长记为
条边的边长记为 ,此四边形内任一点
,此四边形内任一点 到第
到第 条边的距离为
条边的距离为 ,若
,若 ,则
,则 ;根据以上性质,体积为
;根据以上性质,体积为 的三棱锥的第
的三棱锥的第 个面的面积为
个面的面积为 ,此三棱锥内任一点
,此三棱锥内任一点 到
到 个面的距离为
个面的距离为 ,若
,若 ,则
,则 .
.
有一段演绎推理:“直线平行于平面,则这条直线平行于平面内所有直线;直线 ∥平面
∥平面 ,直线
,直线 ;则直线
;则直线 ∥直线
∥直线 ”的结论是错误的原因是: ( )
”的结论是错误的原因是: ( )
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.非以上错误 |
在平面直角坐标系上,设不等式组 所表示的平面区域为
所表示的平面区域为 ,记
,记 内的整点(即横坐标和纵坐标均为整数的点)的个数为
内的整点(即横坐标和纵坐标均为整数的点)的个数为 .则
.则 = ,经猜想可得到
= ,经猜想可得到 = .
= .
下面几种推理过程是演绎推理的是 ( )
A.两条直线平行,同旁内角互补,若∠A和∠B是两条平行直线的同旁内角则 |
| B.由平面三角形的性质,推测空间四面体性质 |
| C.某校高三有10个班,1班51人,2班53人,三班52人,由此推测各班都超过50人 |
D.在数列 中, 中, ,由此推出 ,由此推出 的通项公式 的通项公式 |
观察下列各式:
1=12,
2+3+4=32,
3+4+5+6+7=52,
4+5+6+7+8+9+10=72,
…,可以得出的一般结论是( )
| A.n+(n+1)+(n+2)+…+(3n-2)=n2 |
| B.n+(n+1)+(n+2)+…+(3n-2)=(2n-1)2 |
| C.n+(n+1)+(n+2)+…+(3n-1)=n2 |
| D.n+ (n+1)+(n+2)+…+(3n-1)=(2n-1)2 |
由直线与圆相切时,圆心到切点连线与直线垂直,想到平面与球相切时,球心与切点连线与平面垂直,用的是 ( )
| A.归纳推理 | B.演绎推理 | C.类比推理 | D.传递性推理 |
(本小题满分16分)图(1)、(2)、(3)、(4)分别包含1个、5个、13个、25个第二十九届北京奥运会吉祥物“福娃迎迎”,按同样的方式构造图形,设第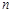 个图形包含
个图形包含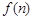 个“福娃迎迎”.
个“福娃迎迎”.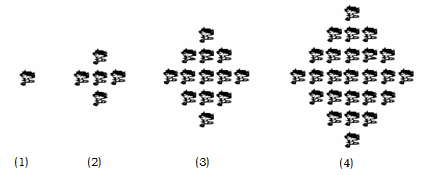
(1)求出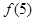 ;
;
(2)利用合情推理的“归纳推理思想”归纳出 与
与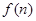 的关系式(不需写出证明过程);
的关系式(不需写出证明过程);
(3)根据你得到的关系式求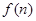 的表达式.
的表达式.
求“方程 的解”有如下解题思路:设
的解”有如下解题思路:设 ,则
,则 在
在 上单调递减,且
上单调递减,且 ,所以原方程有唯一解
,所以原方程有唯一解 .类比上述解题思路,方程
.类比上述解题思路,方程 的解为 .
的解为 .
将演绎推理“函数 的图像是一条直线.”恢复成完全的三段论形式,其中大前提是 .
的图像是一条直线.”恢复成完全的三段论形式,其中大前提是 .
试题篮
()