某产品的广告费用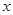 与销售额
与销售额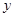 的统计数据如下表:
的统计数据如下表:
广告费用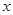 (万元) (万元) |
4 |
2 |
3 |
5 |
销售额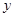 (万元) (万元) |
49 |
26 |
39 |
54 |
根据上表数据预计广告费用为6万元时,销售额为( )
A.63.6万元 B.65.5万元 C.67.7万元 D.72.0万元
工人月工资 (元)与劳动生产率 (千元)变化的回归方程为 ,下列判断正确的是.
①劳动生产率为1千元时,工资为130元;
②劳动生产率提高1千元,则工资提高80元;
③劳动生产率提高1千元,则工资提高130元;
④当月工资为210元时,劳动生产率为2千元.
在两个变量 与
与 的回归模型中,分别选择了4个不同的模型,它们的相关指数R2如下,其中拟合效果最好的模型是
的回归模型中,分别选择了4个不同的模型,它们的相关指数R2如下,其中拟合效果最好的模型是
| A.模型1的相关指数R2为0.98 | B.模型2的相关指数R2为0.90 |
| C.模型3的相关指数R2为0.60 | D.模型4的相关指数R2为0.25 |
若变量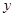 与
与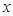 之间的相关系数
之间的相关系数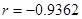 ,则变量
,则变量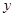 与
与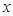 之间
之间
| A.不具有线性相关关系 |
| B.具有线性相关关系 |
| C.它们的线性相关关系还需要进一步确定 |
| D.不确定 |
下表是降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对应数据,根据表中提供的数据,求出y关于x的线性回归方程 =0.7x+0.35,那么表中m的值为( )
=0.7x+0.35,那么表中m的值为( )
| A.4 | B.3.15 | C.4.5 | D.3 |
将容量为n的样本中的数据分成6组,绘制成频率分布直方图,若第一组至第六组数据的频率之比为2:3:4:6:4:1,且前三组数据的频率之和等于27,则n等于 .
某单位为了了解用电量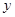 (度)与当天平均气温
(度)与当天平均气温 (°C)之间的关系,随机统计了某4天的当天平均气温与用电量(如右表)。由数据运用最小二乘法得线性回归方程
(°C)之间的关系,随机统计了某4天的当天平均气温与用电量(如右表)。由数据运用最小二乘法得线性回归方程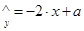 ,则
,则 __________.
__________.
平均气温 (°C) (°C) |
18 |
13 |
10 |
-1 |
用电量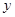 (度) (度) |
25 |
35 |
37 |
63 |
一名小学生的年龄和身高(单位:cm)的数据如下表:

由散点图可知,身高 与年龄
与年龄 之间的线性回归方程为
之间的线性回归方程为 ,则
,则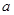 的值为( )
的值为( )
| A.65 | B.74 | C.56 | D.47 |
我国科研人员屠呦呦法相从青篙中提取物青篙素抗疟性超强,几乎达到100%,据监测:服药后每毫升血液中的含药量y(微克)与时间r(小时)之间近似满足如图所示的曲线
(1)写出第一服药后y与t之间的函数关系式y=f(x);
(2)据进一步测定:每毫升血液中含药量不少于 微克时,治疗有效,求服药一次后治疗有效的时间是多长?
微克时,治疗有效,求服药一次后治疗有效的时间是多长?
某产品的广告费用x与销售额y的统计数据如下表:根据上表可得回归方程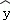 =
=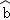 x+a中的b=10.6,据此模型预报广告费用为10万元时销售额为( )
x+a中的b=10.6,据此模型预报广告费用为10万元时销售额为( )
| 广告费用x(万元) |
4 |
2 |
3 |
5 |
| 销售额y(万元) |
49 |
26 |
39 |
58 |
A.112.1万元 B.113.1万元 C.111.9万元 D.113.9万元
某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如右数据:
单价 (元) (元) |
8 |
8.2 |
8.4 |
8.6 |
8.8 |
9 |
销量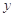 (件) (件) |
90 |
84 |
83 |
80 |
75 |
68 |
由表中数据,求得线性回归方程为 .若在这些样本点中任取一点,则它在回归直线左下方的概率为_______.
.若在这些样本点中任取一点,则它在回归直线左下方的概率为_______.
观察下列关于两个变量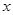 和
和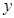 的三个散点图,它们从左到右的对应关系依次为( ).
的三个散点图,它们从左到右的对应关系依次为( ).
| A.正相关、负相关、不相关 |
| B.负相关、不相关、正相关 |
| C.负相关、正相关、不相关 |
| D.正相关、不相关、负相关 |
试题篮
()