某公司的广告费支出x与销售额y(单位:万元)之间有下列对应数据
| x |
2 |
4 |
5 |
6 |
8 |
| y |
30 |
40 |
60 |
50 |
70 |
(1)画出散点图,并判断广告费与销售额是否具有相关关系;
(2)根据表中提供的数据,用最小二乘法求出y与x的回归方程 ;
;
(3)预测销售额为115万元时,大约需要多少万元广告费。
参考公式:回归方程为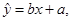 其中
其中 ,
, 
下表为某班5位同学身高x(单位:cm)与体重y(单位kg)的数据,
| 身高 |
170 |
171 |
166 |
178 |
160 |
| 体重 |
75 |
80 |
70 |
85 |
65 |
若两个量间的回归直线方程为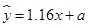 ,则身高为185cm的学生的体重约为( )
,则身高为185cm的学生的体重约为( )
A.87.6kg B.89.5kg C.91.4kg D.92.3kg
设某大学的女生体重 (单位:
(单位: )与身高
)与身高 (单位:
(单位: )具有线性相关关系,根据一组样本数据
)具有线性相关关系,根据一组样本数据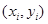 (
( ),用最小二乘法建立的回归方程为
),用最小二乘法建立的回归方程为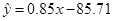 ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )
A. 与 与 具有正的线性相关关系 具有正的线性相关关系 |
B.回归直线过样本点的中心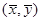 |
C.若该大学某女生身高增加 ,则其体重约增加 ,则其体重约增加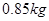 |
D.若该大学某女生身高为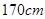 ,则可断定其体重为 ,则可断定其体重为 |
对具有线性相关关系的变量 和
和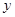 ,测得一组数据如下:
,测得一组数据如下:
| x |
2 |
4 |
5 |
6 |
8 |
| y |
30 |
40 |
60 |
50 |
70 |
若已求得它们的回归方程的斜率为6.5,则这条直线的回归方程为 .
下表是某厂1~4月份用水量(单位:百吨)的一组数据:
| 月份x |
1 |
2 |
3 |
4 |
| 用水量y |
4.5 |
4 |
3 |
2.5 |
由散点图可知,用水量y与月份x之间有较好的线性相关关系,其线性回归直线方程是y=-0.7x+a,则a等于________.
对于下列表格所示的五个散点,已知求得的线性回归直线方程为 =0.8x-155.
=0.8x-155.
| x |
196 |
197 |
200 |
203 |
204 |
| y |
1 |
3 |
6 |
7 |
m |
则实数m的值为( )
A.8.4 B.8.2 C.8 D.8.5
在一组样本数据(x1,y1),(x2,y2),…,(xn,yn)(n≥2,x1,x2,…,xn不全相等)的散点图中,若所有样本点(xi,yi)(i=1,2,…,n)都在直线y= x+1上,则这组样本数据的样本相关系数为 .
x+1上,则这组样本数据的样本相关系数为 .
某咖啡厂为了了解热饮的销售量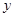 (个)与气温
(个)与气温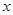 (℃)之间的关系,随机统计了某4天的销售量与气温,并制作了对照表:
(℃)之间的关系,随机统计了某4天的销售量与气温,并制作了对照表:
| 气温(℃) |
18 |
13 |
10 |
-1 |
| 销售量个) |
24 |
34 |
38 |
64 |
由表中数据,得线性回归方程为y= x
x ,,当气温为-4℃时,预测销售量约为
,,当气温为-4℃时,预测销售量约为
A.68 B.66 C.72 D.70
从某高中随机选取5名高三男生,其身高和体重的数据如下表所示:
身高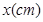 |
160 |
165 |
170 |
175 |
180 |
体重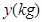 |
63 |
66 |
70 |
72 |
74 |
根据上表可得回归直线方程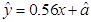 ,据此模型预报身高为172
,据此模型预报身高为172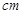 的高三男生的体重为 ( )
的高三男生的体重为 ( )
A.70.09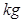 B.70.12
B.70.12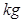 C.70.55
C.70.55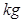 D.71.05
D.71.05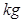
设有一个回归直线方程为 ,则变量x增加一个单位时
,则变量x增加一个单位时
| A.y平均增加1.5个单位 | B.y平均增加2个单位 |
| C.y平均减少1.5个单位 | D.y平均减少2个单位 |
四名同学根据各自的样本数据研究变量 之间的相关关系,并求得回归直线方程,分别得到以下四个结论:
之间的相关关系,并求得回归直线方程,分别得到以下四个结论:
①y与x负相关且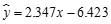 ;
;
②y与x负相关且 ;
;
③y与x正相关且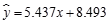 ;
;
④y与x正相关且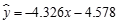 .
.
其中一定不正确的结论的序号是 ( )
| A.①② | B.②③ | C.③④ | D.①④ |
已知某回归直线过点 ,且样本数据中
,且样本数据中 和
和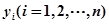 的均值分别为
的均值分别为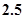 和
和 ,则此回归直线方程为 .
,则此回归直线方程为 .
【改编题】已知x,y的值如下表所示:
| x |
2 |
3 |
4 |
| y |
5 |
4 |
6 |
如果y与x呈线性相关,则回归方程为 所表示的直线经过的定点为_______.
所表示的直线经过的定点为_______.
试题篮
()