为研究学生物理成绩与数学成绩是否相关,某中学老师将一次考试中无名学生的数学、物理成绩记录如下表所示:
根据上表提供的数据,经检验物理成绩与数学成绩呈线性相关,且得到y关于x的线性回归方程 ,那么表中t的值为( )
,那么表中t的值为( )
| A.88 | B.89 | C.90 | D.93 |
若变量 与
与 之间的相关系数
之间的相关系数 ,则变量
,则变量 与
与 之间( )
之间( )
| A.不具有线性相关关系 |
| B.具有线性相关关系 |
| C.它们的线性相关关系还需要进一步确定 |
| D.不确定 |
由变量 与
与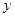 相对应的一组数据
相对应的一组数据 、
、 、
、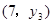 、
、 、
、
得到的线性回归方程为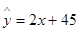 ,则
,则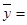 ( )
( )
A.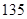 |
B. |
C. |
D. |
登山族为了了解某山高y(km)与气温x(°C)之间的关系,随机统计了4次山高与相应的气温,并制作了对照表:
| 气温x(°C) |
18 |
13 |
10 |
-1 |
| 山高y(km) |
24 |
34 |
38 |
64 |
由表中数据,得到线性回归方程 ,由此请估计出山高为72(km)处气温的度数为()
,由此请估计出山高为72(km)处气温的度数为()
A.-10
B.-8
C.-4
D.-6
某批发市场对某件商品(成本为5元/件)进行了6天的试销,得到如下数据:
单价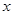 (元) (元) |
8.00 |
8.20 |
8.40 |
8.60 |
8.80 |
9.00 |
销量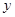 (件) (件) |
90 |
84 |
83 |
80 |
75 |
68 |
经分析发现销量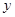 (件)与单价
(件)与单价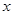 (元)具有线性相关关系,且回归直线方程为
(元)具有线性相关关系,且回归直线方程为 (其中,
(其中,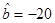 ,
, ),那么今后为了获得最大利润,该商品的的单价应定为 元.
),那么今后为了获得最大利润,该商品的的单价应定为 元.
下表是某厂1~4月份用水量(单位:百吨)的一组数据:
| 月份x |
1 |
2 |
3 |
4 |
| 用水量y |
4.5 |
4 |
3 |
2.5 |
由散点图可知,用水量y与月份x之间有较好的线性相关关系,其线性回归直线方程是y=-0.7x+a,则a等于________.
从某高中随机选取5名高三男生,其身高和体重的数据如下表所示:
| 身高x(cm) |
160 |
165 |
170 |
175 |
180 |
| 体重y(kg) |
63 |
66 |
70 |
72 |
74 |
根据上表可得回归直线方程 ,据此模型预报身高为172cm的高三男生的体重为 ( )
,据此模型预报身高为172cm的高三男生的体重为 ( )
A.70.09kg B.70.12kg C.70.55kg D.71.05kg
从某高中随机选取5名高三男生,其身高和体重的数据如下表所示,
身高 |
160 |
165 |
170 |
175 |
180 |
体重 |
63 |
66 |
70 |
72 |
74 |
由上表可得回归直线方程 ,据此模型预报身高为
,据此模型预报身高为 的男生的体重大约为( )
的男生的体重大约为( )
A.70.09  B.70.12
B.70.12  C.70.55
C.70.55  D.71.05
D.71.05 
如果某地的财政收入x与支出y满足线性回归方程y=a+bx+ε(单位:亿元),其中b=0.8,a=2,|ε|≤0.5.若今年该地区的财政收入为10亿元,则年支出预计不会超出________亿元.
某单位为了解用电量y度与气温x℃之间的关系,随机统计了某4天的用电量与当天气温.
| 气温(℃) |
14 |
12 |
8 |
6 |
| 用电量(度) |
22 |
26 |
34 |
38 |
由表中数据得线性回归方程 =
= x+
x+ 中
中 =-2,据此预测当气温为5 ℃时,用电量的度数约为________.
=-2,据此预测当气温为5 ℃时,用电量的度数约为________.
甲、乙两名同学在 次体育测试中的成绩统计如茎叶图所示,若甲、乙两人的平均成绩分别为
次体育测试中的成绩统计如茎叶图所示,若甲、乙两人的平均成绩分别为 ,则下列结论正确的是( )
,则下列结论正确的是( )
A. ;乙比甲成绩稳定 ;乙比甲成绩稳定 |
B. ;甲比乙成绩稳定 ;甲比乙成绩稳定 |
C. ;甲比乙成绩稳定 ;甲比乙成绩稳定 |
D. ;乙比甲成绩稳定 ;乙比甲成绩稳定 |
某企业对自己的拳头产品的销售价格(单位:元)与月销售量(单位:万件)进行调查,其中最近五个月的统计数据如下表所示:
价格 |
9 |
 |
 |
 |
11 |
销售量 |
11 |
 |
8 |
6 |
5 |
由散点图可知,销售量 与价格
与价格 之间有较强的线性相关关系,其线性回归直线方程是:
之间有较强的线性相关关系,其线性回归直线方程是: ,且
,且 ,则
,则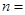 ___
___
若下表数据对应的 关于
关于 的线性回归方程为
的线性回归方程为 ,则
,则 = .
= .
 |
3 |
4 |
5 |
6 |
 |
2.5 |
3 |
4 |
4.5 |
试题篮
()