高中数学合情推理和演绎推理试题

已知正三角形内切圆的半径是其高的，把这个结论推广到空间正四面体，类似的结论是______________________________________．

有一段“三段论”，推理是这样的：对于可导函数，如果，那么 是函数的极值点．因为在处的导数值，所以是函数的极值点．以上推理中 （ ）

A．大前提错误

B．小前提错误

C．推理形式错误

D．结论正确

对于实数，表示不超过的最大整数，观察下列等式：

按照此规律第个等式的等号右边的结果为           ．

面积为的平面凸四边形的第条边的边长记为 ，此四边形内任一点到第条边的距离为，若，则；根据以上性质，体积为的三棱锥的第个面的面积为，此三棱锥内任一点到个面的距离为，若，则           ．

二维空间中圆的一维测度（周长），二维测度（面积），观察发现；三维空间中球的二维测度（表面积），三维测度（体积），观察发现．已知四维空间中“超球”的三维测度，猜想其四维测度______．

观察下列各式：
1＝1²，
2＋3＋4＝3²，
3＋4＋5＋6＋7＝5²，
4＋5＋6＋7＋8＋9＋10＝7²，
…，可以得出的一般结论是（    ）

A．n＋(n＋1)＋(n＋2)＋…＋(3n－2)＝n^2

B．n＋(n＋1)＋(n＋2)＋…＋(3n－2)＝(2n－1)^2

C．n＋(n＋1)＋(n＋2)＋…＋(3n－1)＝n^2

D．n＋ (n＋1)＋(n＋2)＋…＋(3n－1)＝(2n－1)^2

已知不等式，照此规律总结出第个不等式为______________；

把正整数按照下面的表格进行排列

1	3	6	10	15	21
2	5	9	14	20
4	8	13	19
7	12	18
11	17
16

 
则排在第6行，第4列的数是_______________；
排在第行，第列（）的数是______________

已知（），计算得，，，，，由此推算：当时，有（   ）

A．（）

B．（）

C．（）

D．（）

观察下列等式：
                      
                   
                
            
         
                         
可以推测：         ．（，结果用含有的代数式表示）

如图所示的三角形数阵叫“牛顿调和三角形”，它们是由整数的倒数组成的，第n行有n个数且两端的数均为，每个数是它下一行左右相邻两数的和，如 
，…，

则（1）第6行第2个数（从左往右数）为_________；
（2）第n行第3个数（从左往右数）为_________．

已知，由不等式我们可以得出推广结论：，则（ ）   

A．

B．

C．

D．

设函数f (x)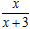＝ (x＞0)，观察：f ₁(x)＝f (x)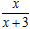＝， f ₂(x)＝f (f ₁(x))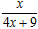＝，f ₃(x)＝f (f ₂(x))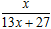＝，f ₄(x)＝f (f ₃(x))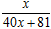＝……，根据以上事实，由归纳推理可得：当n∈N^*，n≥2时，f_n(x)＝f (f_n－1(x))＝           .

如下图所示将若干个点摆成三角形图案，每条边（包括两个端点）有n（n>l，n∈N^*）个点，相应
的图案中总的点数记为，则=（  ）

A．

B．

C．

D．

的所有正约数之和可按如下方法得到：因为，所以的所有正约数之和为，参照上述方法，可求得的所有正约数之和为          ．