高中数学合情推理和演绎推理试题

36的所有正约数之和可按如下方法得到：因为，所以36的所有正约数之和为

参照上述方法，可求得200的所有正约数之和为                    .

观察下列各式：，，，，，，则（   ）

A．28

B．

C．

D．

已知等式“”、“ ”、“ ”均成立．则      ．

已知正三角形内切圆的半径与它的高的关系是：，把这个结论推广到空间正四面体，则正四面体内切球的半径与正四面体高的关系是        ． 

已知集合，且下列三个关系：‚有且只有一个正确，则.

观察下列等式：

可以推测：1³＋2³＋3³＋…＋n³＝________(n∈N^*，用含n的代数式表示)．

设等差数列{a_n}的前n项和为S_n，则S₄，S₈－S₄，S₁₂－S₈，S₁₆－S₁₂成等差数列．类比以上结论有：设等比数列{b_n}的前n项积为T_n，则T₄，________，________，成等比数列．

观察下列不等式：①<1；②＋<；③＋＋<；….则第n个不等式为________．

给出下面类比推理命题(其中Q为有理数集，R为实数集，C为复数集)：
①“若a，b∈R，则a－b＝0⇒a＝b”，类比推出“若a，b∈C，则a－b＝0⇒a＝b”；
②“若a，b，c，d∈R，则复数a＋bi＝c＋di⇒a＝c，b＝d”，类比推出，“若a，b，c，d∈Q，则a＋b＝c＋d⇒a＝c，b＝d”；
③“若a，b∈R，则a－b>0⇒a>b”，类比推出“若a，b∈C，则a－b>0⇒a>b”；
④“若x∈R，则|x|<1⇒－1<x<1”，类比推出“若z∈C，则|z|<1⇒－1<z<1”．
其中类比正确的为(　　)

A．①②

B．①④

C．①②③

D．②③④

观察下列各式：a＋b＝1，a²＋b²＝3，a³＋b³＝4，a⁴＋b⁴＝7，a⁵＋b⁵＝11，…，则a¹⁰＋b¹⁰＝(　　)

A．28

B．76

C．123

D．199

设，，由计算得，，，，观察上述结果，可推出一般的结论为           .

1955年，印度数学家卡普耶卡（D.R.Kaprekar）研究了对四位自然数的一种交换：任给出四位数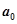，用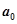的四个数字由大到小重新排列成一个四位数m，再减去它的反序数n(即将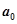的四个数字由小到大排列，规定反序后若左边数字有0，则将0去掉运算，比如0001，计算时按1计算)，得出数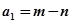，然后继续对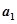重复上述变换，得数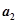，…，如此进行下去，卡普耶卡发现，无论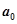是多大的四位数，只要四个数字不全相同，最多进行k次上述变换，就会出现变换前后相同的四位数t(这个数称为Kaprekar变换的核).通过研究10进制四位数2014可得Kaprekar变换的核为             .

在平面上，到直线的距离等于定长的点的轨迹是两条平行直线.类比在空间中：
（1）到定直线的距离等于定长的点的轨迹是        ；
（2）到已知平面相等的点的轨迹是        .

已知△ABC中，，求证：.证明：∴，其中，画线部分是演绎推理的（   ）

A．小前提

B．大前提

C．结论

D．三段论

观察，，，由归纳推理可得：若定义在上的函数满足，记为的导函数，则（   ）

A．

B．

C．

D．