由“正三角形的内切圆切于三边的中点”,可类比猜想出正四面体的内切球切于四个侧面( )
| A.各正三角形内任一点 | B.各正三角形的某高线上的点 |
| C.各正三角形的中心 | D.各正三角形外的某点 |
下面三段话可组成 “三段论”,则“小前提”是()
① 因为指数函数y =" a" x(a > 1 )是增函数;②所以y = 2x是增函数;
③ 而y = 2x是指数函数。
| A.① | B.② | C.③ | D. ①② |
观察(x2)'=2x,(x4)'=4x3,(cosx)'= -sinx,由归纳推理可得:若定义在R上的函数f(x)满足f(-x)=f(x),记g(x)为f(x)的导函数,则g(-x)等于( )
| A.f(x) | B.-f(x) | C.g(x) | D.-g(x) |
下面几种推理过程是演绎推理的是( )
A.两条直线平行,同旁内角互补,如果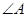 和 和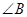 是两条平行直线的同旁内角,则 是两条平行直线的同旁内角,则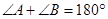 . . |
| B.由平面三角形的性质,推测空间四面体性质. |
| C.某校高二共10个班,1班51人,2班53人,3班52人,由此推测各班都超过50人 |
D.在数列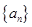 中 中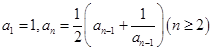 ,由此归纳出 ,由此归纳出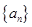 的通项公式. 的通项公式. |
已知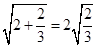 ,
,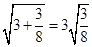 ,
,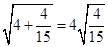 ,。。。,若
,。。。,若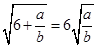 (a , b
(a , b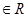 ) , 则( )
) , 则( )
| A.a=5, b=24 | B.a=6, b=24 |
| C.a=6, b=35 | D.a=5, b=35 |
在平面几何里,有勾股定理:“设 的两边
的两边 互相垂直,则
互相垂直,则 ”拓展到空间,类比平面几何的勾股定理,“设三棱锥
”拓展到空间,类比平面几何的勾股定理,“设三棱锥 的三个侧面
的三个侧面 、
、 、
、 两两互相垂直”,则可得 ( )
两两互相垂直”,则可得 ( )
A. |
B. |
C. |
D. |
下列推理是类比推理的是( )
A.由数列 ,猜测出该数列的通项为 ,猜测出该数列的通项为 |
| B.平面内不共线的三点确定一个圆,由此猜想空间不共面的三点确定一个球 |
C.垂直于同一平面的两条直线平行,又直线 ,直线 ,直线 ,推出 ,推出 |
D.由 ,推出 ,推出 |
对“a,b,c是不全相等的正数”,给出如下判断:
①(a-b)2+(b-c)2+(c-a)2≠0;②a>b与a<b及a=b中至少有一个成立;
③a≠c,b≠c,a≠b不能同时成立,其中判断正确的个数是( )
| A.0 | B.1 | C.2 | D.3 |
观察下列各式: . , , , ,则 ()
| A. | 28 | B. | 76 | C. | 123 | D. | 199 |
有一段演绎推理是这样的:“三角函数是周期函数, 是三角函数,所以
是三角函数,所以 是周期函数.”在以上演绎推理中,下列说法正确的是( )
是周期函数.”在以上演绎推理中,下列说法正确的是( )
| A.推理完全正确 | B.大前提不正确 |
| C.小前提不正确 | D.推理形式不正确 |
已知结论:“在正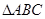 中,
中,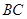 中点为
中点为 ,若
,若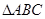 内一点
内一点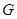 到各边的距离都相等,则
到各边的距离都相等,则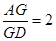 ”.若把该结论推广到空间,则有结论:“在棱长都相等的四面体
”.若把该结论推广到空间,则有结论:“在棱长都相等的四面体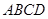 中,若
中,若 的中心为
的中心为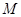 ,四面体内部一点
,四面体内部一点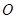 到四面体各面的距离都相等,则
到四面体各面的距离都相等,则 ( ▲ )
( ▲ )
| A.1 | B.2 | C.3 | D.4 |
试题篮
()